题目内容
11. 如图,线段AB是半径为6的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上(AM<BN),MN=5.若∠MCN=45°,线段AM的长度为3或4.
如图,线段AB是半径为6的⊙O的直径,点C是弧AB的中点,点M、N在线段AB上(AM<BN),MN=5.若∠MCN=45°,线段AM的长度为3或4.
分析 作DA⊥AB,使DA=BN,连接DC,DM,根据旋转的性质求得∠ACD=∠BCN,DC=NC,然后证得△DMC≌△NMC,求得DM=MN=5,设AM=x;则AD=BN=AB-AM-MN=7-x,根据勾股定理得出x2+(7-x)2=25,进而就可求得线段AM的长度.
解答 解:作DA⊥AB,使DA=BN,连接DC,DM,
∵线段AB是⊙O的直径,点C是弧AB的中点,
∴$\widehat{AC}$=$\widehat{BC}$,∠ACB=90°,
∴AC=BC,
∴∠CAB=∠CBA=45°,
∴∠DAC=∠NBC=45°,
在△ADC和△NCB中,$\left\{\begin{array}{l}{AD=BN}\\{∠DAC=∠NBC}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△NCB(SAS),
∴∠ACD=∠BCN,DC=NC,
∵∠MCN=45°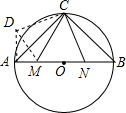
∴∠ACM+∠BCN=45°
∴∠ACM+∠ACD=45°
即∠MCD=45°=∠MCN,
在△DMC和△NMC中,$\left\{\begin{array}{l}{DC=CN}\\{∠MCD=∠MCN}\\{CM=CM}\end{array}\right.$,
∴△DMC≌△NMC(SAS),
∴DM=MN=5,
设AM=x;则AD=BN=AB-AM-MN=7-x
根据勾股定理
AM2+AD2=DM2
x2+(7-x)2=25,
解得x=3或x=4,
∴AM的长度为3或4.
故答案为:3或4.
点评 本题考查了旋转的性质,三角形全等的判定和性质,等腰直角三角形的性质,勾股定理的应用等,作出辅助线构建全等三角形是解题的关键.

练习册系列答案
相关题目
3. 如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )
如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )
 如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )
如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )| A. | n可以为3和4 | |
| B. | n可以为所有正偶数 | |
| C. | n可以为所有大于2的整数 | |
| D. | 正整数中所有3的倍数的数都可以为n值 |
20.已知线段AB=6cm,点C是直线AB上一点,BC=4cm,则线段AC的长度是( )
| A. | 10cm | B. | 2cm | C. | 2cm或10cm | D. | 5cm |
 已知:点P为正方形ABCD内一点,连接PA、PB、PC,若AP2+CP2=2PB2,
已知:点P为正方形ABCD内一点,连接PA、PB、PC,若AP2+CP2=2PB2,