��Ŀ����
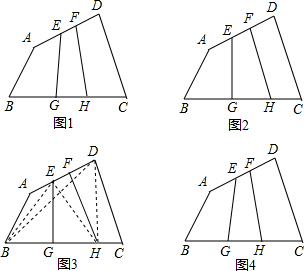
18��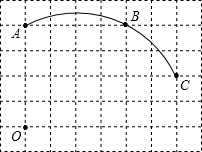 ��ͼ���ڵ�λ����Ϊ1�������������У�һ��Բ���������A��B��C��
��ͼ���ڵ�λ����Ϊ1�������������У�һ��Բ���������A��B��C����1��������Բ������Բ��Բ��D��λ�ã�����д������������ͼ�ۼ�����������AD��CD��
��2�����ڣ�1���Ļ����ϣ�����������⣺
���Ե�OΪԭ�㡢ˮƽ��������ֱ��Ϊx�ᡢ��ֱ��������ֱ��Ϊy�ᣬ����ƽ��ֱ������ϵ��д��������꣺C��6��2����D��2��0����
�ڡ�D�İ뾶Ϊ2$\sqrt{5}$������������ţ���
����������ADCΧ��һ��Բ�IJ��棬���Բ�ĵ���Բ�뾶��$\frac{\sqrt{5}}{2}$��
����E��7��0�������ж�ֱ��EC���D��λ�ù�ϵ��˵��������ɣ�
���� ��1���������⽨��ƽ��ֱ������ϵ��Ȼ��������AB�Ĵ�ֱƽ���ߣ��Լ�BC�Ĵ�ֱƽ���ߣ���ֱ�ߵĽ��㼴ΪԲ��D������AD��CD��
��2���ٸ��ݵ�һ�ʻ�����ͼ�μ��ɵó�C��D�����ꣻ
����ֱ��������AOD�У���OA��OD�ij������ù��ɶ������AD�ij�����ΪԲO�İ뾶��
�������ADC�Ķ������û�ADC���ܳ������Բ�ĵ���뾶���ɣ�
��ֱ��CE��ԲO��λ�ù�ϵ�����У�����Ϊ����Բ�İ뾶�ó�DC�ij�����ֱ��������CEF�У���CF��FE�ij������ù��ɶ������CE�ij�������DE�ij������ù��ɶ������涨���ó�������DCEΪֱ�������Σ���EC��ֱ��DC���ɵó�ֱ��CEΪԲO�����ߣ�
��� 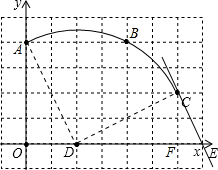 �⣺��1���������⻭����Ӧ��ͼ�Σ���ͼ��ʾ��
�⣺��1���������⻭����Ӧ��ͼ�Σ���ͼ��ʾ��
��2���ٸ���ͼ�εã�C��6��2����D��2��0����
����Rt��AOD��OA=4��OD=2��
���ݹ��ɶ����ã�AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=2$\sqrt{5}$��
���D�İ뾶Ϊ2$\sqrt{5}$��
��AC=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$��CD=2$\sqrt{5}$��
AD2+CD2=AC2��
���ADC=90�㣮
����ADC�Ļ���=$\frac{90�С�2\sqrt{5}}{180}$=$\sqrt{5}$�У�
Բ�ĵ���İ뾶=$\frac{\sqrt{5}}{2}$��
��ֱ��EC���D��λ�ù�ϵΪ���У�����Ϊ��
��Rt��CEF��CF=2��EF=1��
���ݹ��ɶ����ã�CE=$\sqrt{C{F}^{2}+E{F}^{2}}$=$\sqrt{5}$��
�ڡ�CDE�У�CD=2$\sqrt{5}$��CE=$\sqrt{5}$��DE=5��
��CE2+CD2=��$\sqrt{5}$��2+��2$\sqrt{5}$��2=5+20=25��DE2=25��
��CE2+CD2=DE2��
���CDEΪֱ�������Σ�����DCE=90�㣬
��CE��DC��
��CE��ԲD���У�
�ʴ�Ϊ���٣�6��2������2��0������2$\sqrt{5}$����$\frac{\sqrt{5}}{2}$��
���� ���⿼����ֱ����Բ��λ�ù�ϵ���漰��֪ʶ�У�������ͼ�����ʣ��������������ɶ������涨�������ߵ��ж������������ν�ϵ�˼�룬�������⻭����Ӧ��ͼ���ǽⱾ��Ĺؼ���

 ͬ��ѧ��һ�ζ���ϵ�д�
ͬ��ѧ��һ�ζ���ϵ�д� �����ܾ�ϵ�д�
�����ܾ�ϵ�д� ���ƿ�����ϵ�д�
���ƿ�����ϵ�д� ���¿쳵����������ϵ�д�
���¿쳵����������ϵ�д����μ��棬ͨ��������ʾ���ʵ�������ʱ�������ȣ��������й�������еĸ��ܣ�9��1�տ�ѧʱ����ʦΪ����ȫ����ͬѧ������ʶ�������41λͬѧ�˴�����Ϊ��ͬʱ�˴˽����Լ�����һ��������ͬѧ��ɹ�������ʦ���һ�����⣺��˭֪�����ղ�ȫ��ͬѧ�ܹ����ּ��Σ���С��ͬѧ��������˵820�Σ���˵�ĶԲ��ԣ�
̽���о�
��ʵҪ����������⣬���������µķ���������������������ˣ�����������߶���Ŀ���ͱ�ʾ���ֵĴ����� ���ǿ�����һ���ɵ���߶���ɵ�ͼ������һ��
| ����ͼ�� | �������� | ���ִ��� |
 | 2 | 1 |
 | 3 | 3=1+2 |
 | 4 | 6=1+2+3 |
 | 5 | 10=1+2+3+4 |
| �� | �� | �� |
| �� | N | P=1+2+3+��+��n+1�� |
�������
����41λͬѧ�˴�����Ϊ�����ǹ����ֶ��ٴΣ�С��ͬѧ˵�ĶԲ��ԣ�
������չ
�����÷��������������о�ƽ����n��ֱ������ж��ٸ����㣿��������±���
| ͼ�� | ֱ������ | ������� |
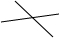 | 2 | 1 |
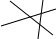 | 3 | 3=1+2 |
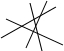 | 4 | |
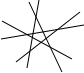 | 5 | |
| �� | �� | �� |
| �� | n |
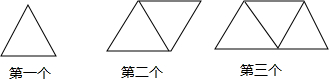
��1������±������
| ��������� | 1 | 2 | 3 | 4 | �� | n |
| �������� | 3 | 5 | 7 | 9 | �� | 2n+1 |
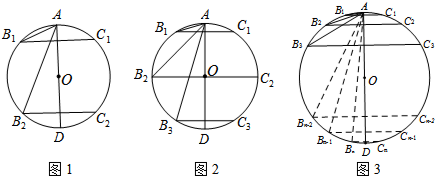
 ��������⡿��ͼ�٣����ı���ABCD�У���E��F��AD��n�ȷֵ������м�2������G��H��BC��n�ȷֵ������м�2����������nΪ������������EG��FH����ôS�ı���EFHG��S�ı���ABCD֮����ʲô��ϵ�أ�
��������⡿��ͼ�٣����ı���ABCD�У���E��F��AD��n�ȷֵ������м�2������G��H��BC��n�ȷֵ������м�2����������nΪ������������EG��FH����ôS�ı���EFHG��S�ı���ABCD֮����ʲô��ϵ�أ�
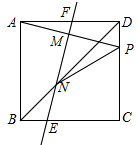 ��ͼ��������ABCD�У���PΪCD��һ�㣬�߶�AP�Ĵ�ֱƽ����MN��BD�ڵ�N����MΪ���㣬�������ڵ�E��F������PN�������н��ۣ�������ȷ���У�������
��ͼ��������ABCD�У���PΪCD��һ�㣬�߶�AP�Ĵ�ֱƽ����MN��BD�ڵ�N����MΪ���㣬�������ڵ�E��F������PN�������н��ۣ�������ȷ���У�������