题目内容
3.如图,两条直线相交只有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,五条直线相交最多有10个交点,八条直线相交最多有28个交点.
分析 根据题意,结合图形,发现:3条直线相交最多有3个交点,4条直线相交最多有6个交点,5条直线相交最多有10个交点.而3=1+2,6=1+2+3,10=1+2+3+4,故可猜想,n条直线相交,最多有1+2+3+…+(n-1)=$\frac{1}{2}$n(n-1)个交点,由此代入得出答案即可.
解答 解:3条直线相交最多有1+2=3个交点,
4条直线相交最多有1+2+3=6个交点,
5条直线相交最多有1+2+3+4=10个交点,
…
n条直线相交,最多有1+2+3+…+(n-1)=$\frac{1}{2}$n(n-1)个交点,
八条直线相交最多有$\frac{1}{2}$×8×(8-1)=28个交点.
故答案为:28.
点评 此题考查图形的变化规律,培养学生的观察、实验和猜想、归纳能力,掌握从特殊向一般猜想的方法.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
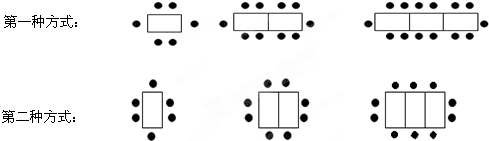
11.观察下图,填表后再回答问题:
(1)在表格中填入正确的数:
(2)试求第6个图形中“●”的个数和“☆”的个数?
(3)试求第n个图形中“●”的个数和“☆”的个数?
| 序号 | 1 | 2 | 3 | … |
| 图形 |  |  |  | … |
| ●的个数 | 8 | 16 | 24 | … |
| ☆的个数 | 1 | 4 | 9 | … |
(2)试求第6个图形中“●”的个数和“☆”的个数?
(3)试求第n个图形中“●”的个数和“☆”的个数?
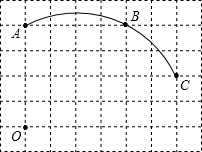 如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.
如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.
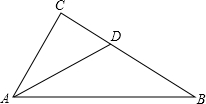 如图,在三角形ABC中,∠C=90度,AD是角平分线,CD=1.5,BD=2.5,求AC的长.
如图,在三角形ABC中,∠C=90度,AD是角平分线,CD=1.5,BD=2.5,求AC的长.