题目内容
8.解下列不等式组(1)$\left\{\begin{array}{l}{x+2(x-1)<4}\\{\frac{1+4x}{3}>x-1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{4(x-0.3)<0.5x+5.8}\\{5-\frac{1}{3}x>-\frac{1}{4}+1}\end{array}\right.$.
分析 (1)先求出各不等式的解集,再求其公共解集即可.
(2)先求出各不等式的解集,再求其公共解集即可.
解答 解:(1)$\left\{\begin{array}{l}{x+2(x-1)<4①}\\{\frac{1+4x}{3}>x-1②}\end{array}\right.$
解①得:x<2.
解②得:x>-4.
∴原不等式组的解集为-4<x<2.
(2)$\left\{\begin{array}{l}{4(x-0,3)<0.5x+5.8①}\\{5-\frac{1}{3}x>-\frac{1}{4}+1②}\end{array}\right.$
解①得:x<2.
解②得:x$<\frac{61}{4}$.
∴原不等式组的解集为<2.
点评 本题考查了解一元一次不等式,解不等式组应遵循的原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列因式分解中,正确的是( )
| A. | x2-9=(x-3)2 | B. | 3a-3b+3=3(a-b) | ||
| C. | -x2+2xy-y2=-(x-y)2 | D. | a2-3a-4=(a+2)(a-2)-3a |
20.若A(-5,y1),B(-3,y2),C(0,y3)为二次函数y=x2+4x-5的图象上的三点,则y1、y2、y3的大小关系是( )
| A. | y2<y3<y1 | B. | y1<y2<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
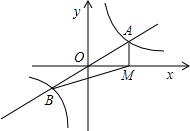 如图,直线y=mx与双曲线交y=$\frac{k}{x}$于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若△ABM的面积等于2,则k的值是( )
如图,直线y=mx与双曲线交y=$\frac{k}{x}$于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若△ABM的面积等于2,则k的值是( )