题目内容
8. 如图,为了测量山顶铁塔AE的高,小明在25m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为58m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
如图,为了测量山顶铁塔AE的高,小明在25m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为58m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
分析 根据楼高和山高可求出EF,继而得出AF,在Rt△AFC中表示出CF,在Rt△ABD中表示出BD,根据CF=BD可建立方程,解方程即可.
解答 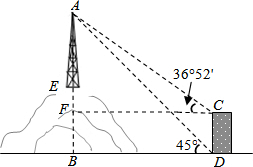 解:如图,过点C作CF⊥AB于点F.
解:如图,过点C作CF⊥AB于点F.
设塔高AE=x,
由题意得,EF=BE-CD=58-25=33m,AF=AE+EF=(x+33)m,
在Rt△AFC中,∠ACF=36°52′,AF=(x+33)m,
则CF=$\frac{AF}{tan36°52′}$≈$\frac{x+33}{0.75}$=$\frac{4}{3}$x+44,
在Rt△ABD中,∠ADB=45°,AB=x+58,
则BD=AB=x+58,
∵CF=BD,
∴$\frac{4}{3}$x+44=x+58,
解得:x=42,
答:该铁塔的高AE为42米.
点评 本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,注意利用方程思想求解,难度一般.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
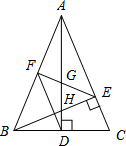 如图,在△ABC中,AB=AC,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确结论的序号是①②③④.(把你认为正确结论的序号都填上).
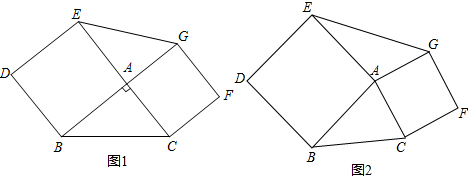
如图,在△ABC中,AB=AC,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确结论的序号是①②③④.(把你认为正确结论的序号都填上).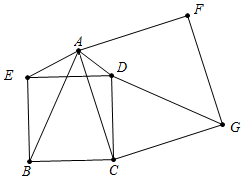 如图,BCDE,ACGF是正方形,三角形AED、CDG的面积分别为4.5与8,那么正方形BCDE的面积是多少?
如图,BCDE,ACGF是正方形,三角形AED、CDG的面积分别为4.5与8,那么正方形BCDE的面积是多少?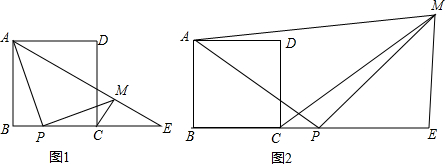
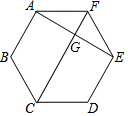 如图,在正六边形ABCDEF中,连接CF,AE,则$\frac{FG}{CG}$的值为$\frac{1}{3}$.
如图,在正六边形ABCDEF中,连接CF,AE,则$\frac{FG}{CG}$的值为$\frac{1}{3}$.