题目内容
2.计算:(1)(2$\sqrt{3}$-3$\sqrt{12}$+6$\sqrt{8}$)÷2$\sqrt{2}$
(2)$\frac{1}{2}$$\sqrt{8}$-$\sqrt{0.5}$-$\sqrt{4\frac{1}{2}}$+2$\sqrt{50}$.
分析 (1)先把括号内的各二次根式化为最简二次根式,然后合并后进行二次根式的除法运算;
(2)先把各二次根式化为最简二次根式,然后合并即可.
解答 解:(1)原式=(2$\sqrt{3}$-6$\sqrt{3}$+12$\sqrt{2}$)÷2$\sqrt{2}$
=(-4$\sqrt{3}$+12$\sqrt{2}$)÷2$\sqrt{2}$
=-$\sqrt{6}$+6;
(2)原式=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$-$\frac{3\sqrt{2}}{2}$+10$\sqrt{2}$
=9$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.下列分式中,无论x取什么值,总有意义的是( )
| A. | $\frac{1}{{x}^{2}+1}$ | B. | $\frac{x}{2x+1}$ | C. | $\frac{1}{{x}^{2}}$ | D. | $\frac{x-5}{x}$ |
11.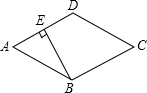 如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )
如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )
 如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )
如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 1 |
 已知2y-3与-3x-1成正比例,且x=2时,y=5.
已知2y-3与-3x-1成正比例,且x=2时,y=5.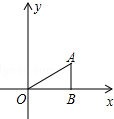 如图,△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O逆时针旋转120°后得到△A1B1O,则点B1的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
如图,△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O逆时针旋转120°后得到△A1B1O,则点B1的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).