题目内容
11.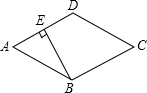 如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )
如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 1 |
分析 根据菱形的性质可求得∠A=60°,在Rt△ABE中由三角函数的定义可求得BE.
解答 解:∵四边形ABCD为菱形,
∴AD∥BC,
∴∠A+∠ABC=180°,
∴∠A=180°-120°=60°,
∵BE⊥AD,
∴sinA=$\frac{BE}{AB}$,
∴BE=AB•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
故选A.
点评 本题主要考查菱形的性质和三角函数的定义,求得∠A的大小是解题的关键,注意三角函数定义的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.下列各组数据中,以它们为边长不能构成直角三角形的是( )
| A. | 3,4,5 | B. | 5,12,13 | C. | $\sqrt{2},\sqrt{2},2$ | D. | 1,2,3 |
3. 如图,已知三角形ABC平移后得到三角形DEF,则下列说法中,不正确的是( )
如图,已知三角形ABC平移后得到三角形DEF,则下列说法中,不正确的是( )
 如图,已知三角形ABC平移后得到三角形DEF,则下列说法中,不正确的是( )
如图,已知三角形ABC平移后得到三角形DEF,则下列说法中,不正确的是( )| A. | AC=DF | B. | BC∥EF | ||
| C. | 平移的距离是线段BD的长 | D. | 平移的距离是线段AD的长 |
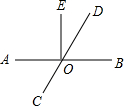 如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=30°,则∠AOC=60°.
如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=30°,则∠AOC=60°. 如图,在平行四边形ABCD中,AC⊥BC,E为AB的中点,若CE=5,AC=8,则AD=6.
如图,在平行四边形ABCD中,AC⊥BC,E为AB的中点,若CE=5,AC=8,则AD=6.
 如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4),将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是y=$\frac{8}{x}$.
如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4),将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是y=$\frac{8}{x}$.