题目内容
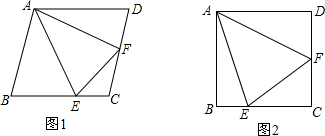
12.如图,在菱形ABCD中,E是BC上一点,F是CD上一点,连接AE、AF、EF,且∠AEB=∠AEF.(1)如图1,求证:AF平分∠EFD;
(2)如图2,若∠C=90°,求证:EF=BE+DF;
(3)在(2)的条件下,若AB=3BE,AE=2$\sqrt{10}$,求AF的长.
分析 (1)根据菱形的性质得出AC平分∠BCD,再根据角平分线的性质证明即可.
(2)根据正方形的性质和全等三角形的判定和性质证明即可;
(3)根据勾股定理进行解答即可.
解答 解:(1)证明:过点A作AG⊥BC于G,过A作AH⊥EF于H,过A作AM⊥CD于M,连接AC,
∵四边形ABCD是菱形,
∴AC平分∠BCD,
又∵AG⊥BC,AM⊥CD,
∴AG=AM,
∵∠AEB=∠AEF,
∴AE平分∠BEF,
又∵AG⊥BC,AH⊥EF,
∴AG=AH,
∴AH=AM,
∴AF平分∠EFD;
(2)∵四边形ABCD是菱形,
又∵∠C=90°,
∴四边形ABCD是正方形,
∴∠B=∠D=90°,
∴AB⊥BC,AD⊥CD,
过A作AH⊥EF于H,
∴∠AHE=∠AHF=90°,
∴AE平分∠BEF,
又∵AB⊥BC,AH⊥EF,
∴AB=AH,
∵AE=AE,
在Rt△ABE与Rt△AHE中
$\left\{\begin{array}{l}{AB=AH}\\{AE=AE}\end{array}\right.$,
∴Rt△ABE≌Rt△AHE(HL)
∴BE=HE,
同理Rt△ADF≌Rt△AHF(HL),
∴DF=HF,
∵EF=EH+FH,
∴EF=BE+DF;
(3)设BE=a,则AB=3a,
在Rt△ABE中,BE2+AB2=AE2,
∴${a}^{2}+(3a)^{2}=(2\sqrt{10})^{2}$,
∴a=2,
∴AB=3a=6,
由(2)知四边形ABCD是正方形,
∴BC=CD=AB=6,
∴CE=BC-BE=4,
设DF=m,则CF=CD-DF=6-m,
由(2)知EF=BE+DF,
∴EF=2+m,
在Rt△ECF中,CE2+CF2=EF2,
∴42+(6-m)2=(2+m)2,
∴m=3,
在Rt△ADF中,DF2+AD2=AF2,
∴$AF=\sqrt{{3}^{2}+{6}^{2}}=3\sqrt{5}$.
点评 此题主要考查了菱形的性质,关键是判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.

 为了了解本校七年级学生的身体素质情况,体育老师随机抽取了本校50名七年级学生进行一分钟跳绳次数测试,测试所得样本数据(单位:次)如下:
为了了解本校七年级学生的身体素质情况,体育老师随机抽取了本校50名七年级学生进行一分钟跳绳次数测试,测试所得样本数据(单位:次)如下:88 90 92 96 99 102 106 108 110 112
113 115 115 117 118 120 120 123 125 127
130 132 134 134 134 135 136 137 138 138
139 141 142 142 143 144 145 146 148 149
150 152 153 157 160 162 162 165 168 172
(1)记跳绳次数为x,补全下面的样本频数分布表与频数分布直方图:
| 组别 | 次数(x) | 频数(人数) |
| 1 | 80≤x<100 | 5 |
| 2 | 100≤x<120 | 10 |
| 3 | 120≤x<140 | 16 |
| 4 | 140≤x<160 | 13 |
| 5 | 160≤x<180 | 6 |
| A. | 15 | B. | 10 | C. | 75 | D. | 3 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
 将一个直角三角板和一把直尺如图放置,如果∠1=38°,则∠2的度数是52度.
将一个直角三角板和一把直尺如图放置,如果∠1=38°,则∠2的度数是52度.