题目内容
4.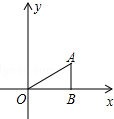 如图,△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O逆时针旋转120°后得到△A1B1O,则点B1的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
如图,△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O逆时针旋转120°后得到△A1B1O,则点B1的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
分析 过B1作B1C⊥y轴于C,由把△ABO绕点O逆时针旋转120°后得到△A1B1O,根据旋转的性质得到∠BOB1=120°,OB1=OB=$\sqrt{3}$,解直角三角形即可得到结果.
解答 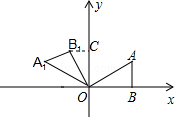 解:过B1作B1C⊥y轴于C,
解:过B1作B1C⊥y轴于C,
∵把△ABO绕点O逆时针旋转120°后得到△A1B1O,
∴∠BOB1=120°,OB1=OB=$\sqrt{3}$,
∵∠BOC=90°,
∴∠COB1=30°,
∴B1C=$\frac{1}{2}$OB1=$\frac{\sqrt{3}}{2}$,OC=$\frac{3}{2}$,
∴B1(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
故答案为:(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 如图,已知三角形ABC平移后得到三角形DEF,则下列说法中,不正确的是( )
如图,已知三角形ABC平移后得到三角形DEF,则下列说法中,不正确的是( )
 如图,已知三角形ABC平移后得到三角形DEF,则下列说法中,不正确的是( )
如图,已知三角形ABC平移后得到三角形DEF,则下列说法中,不正确的是( )| A. | AC=DF | B. | BC∥EF | ||
| C. | 平移的距离是线段BD的长 | D. | 平移的距离是线段AD的长 |
 如图,△ABC中,以AC为直径的⊙O与边AB交于点D,点E为⊙O上一点,连接CE并延长交AB于点F,连接ED.
如图,△ABC中,以AC为直径的⊙O与边AB交于点D,点E为⊙O上一点,连接CE并延长交AB于点F,连接ED. 如图,在正方形网格中有一个边长为4的平行四边形ABCD
如图,在正方形网格中有一个边长为4的平行四边形ABCD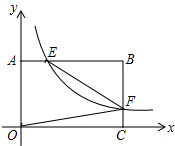 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大. 如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4),将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是y=$\frac{8}{x}$.
如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4),将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是y=$\frac{8}{x}$.