题目内容
10.甲同学用如图方法作出C点,表示数$\sqrt{13}$,在△OAB中,∠OAB=90°,OA=2,AB=3,且点O,A,C在同一数轴上,OB=OC(1)请说明甲同学这样做的理由;
(2)仿照甲同学的做法,在如图所给数轴上描出表示-$\sqrt{29}$的点A.

分析 (1)依据勾股定理求得OB的长,从而得到OC的长,故此可得到点C表示的数;
(2)由29=25+4,依据勾股定理即可做出表示-$\sqrt{29}$的点.
解答 解:(1)在Rt△AOB中,OB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∵OB=OC,
∴OC=$\sqrt{13}$.
∴点C表示的数为$\sqrt{13}$.
(2)如图所示:
取OB=5,作BC⊥OB,取BC=2.
由勾股定理可知:OC=$\sqrt{O{B}^{2}+B{C}^{2}}$=$\sqrt{{5}^{2}+{2}^{2}}$=$\sqrt{29}$.
∵OA=OC=$\sqrt{29}$.
∴点A表示的数为-$\sqrt{29}$.
点评 本题主要考查的是实数与数轴、勾股定理的应用,掌握勾股定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,有一矩形空地,一边是长为20米的墙,另三边是由一根长34米的铁丝围成,且与墙平行的一边有一个1米宽的小门.已知矩形空地的面积是125平方米,求矩形空地的长和宽.
如图,有一矩形空地,一边是长为20米的墙,另三边是由一根长34米的铁丝围成,且与墙平行的一边有一个1米宽的小门.已知矩形空地的面积是125平方米,求矩形空地的长和宽.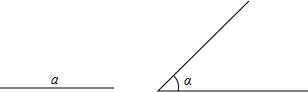 已知线段a和∠α,尺规作图:
已知线段a和∠α,尺规作图: 如图,设P为△ABC内一点,且PC=BC,求证:AB>AP.
如图,设P为△ABC内一点,且PC=BC,求证:AB>AP.