题目内容
某地政府为缓解该地旱情,计划在某租赁公司租借50台掘井机,其中甲型20台,乙型30台.现将这50台掘井机派往A,B两地区,其中30台派往A地区,20台派往B地区.两地区与该租赁公司商定的每天的租赁价格见表:
(1)设派往A地区x台乙型掘井机,租赁公司一天获得的租金为y(元),求y与x之间的函数关系式,并写出x的取值范围;
(2)租赁公司若使这50台掘井机一天获得的租金总额不低于7960元,有多少种分派方案?并将各种方案设计出来;
(3)如果要使这50台掘井机每天获得的租金最高,请你为该租赁公司提出一条合理的建议.
| 每台甲型掘井机的租金 | 每台乙型掘井机的租金 | |
| A地区 | 180元 | 160元 |
| B地区 | 160元 | 120元 |
(2)租赁公司若使这50台掘井机一天获得的租金总额不低于7960元,有多少种分派方案?并将各种方案设计出来;
(3)如果要使这50台掘井机每天获得的租金最高,请你为该租赁公司提出一条合理的建议.
考点:一次函数的应用
专题:
分析:(1)设派往A地区x台乙型掘井机,则派往A地区(30-x)台甲型掘井机,派往B地(30-x)台乙型掘井机,派往B地(x-10)台甲型掘井机,根据总租金=A地两种掘井机的租金+B地两种掘井机的租金就可以表示出y与x之间的函数关系式,由此建立不等式组就可以求出x的取值范围;
(2)由(1)的解析式建立不等式组,求出其解就可以得出结论;
(3)根据(1)的解析式,由一次函数的性质就可以求出最大利润,而得出结论.
(2)由(1)的解析式建立不等式组,求出其解就可以得出结论;
(3)根据(1)的解析式,由一次函数的性质就可以求出最大利润,而得出结论.
解答:解:(1)设派往A地区x台乙型掘井机,则派往A地区(30-x)台甲型掘井机,派往B地(30-x)台乙型掘井机,派往B地(x-10)台甲型掘井机,由题意,得
y=160x+180(30-x)+160(x-10)+120(30-x),
y=20x+7400.
∵
,
∴10≤x≤30;
(2)由题意,得
20x+7400≥7960,
解得:x≥28,
∵10≤x≤30;
∴28≤x≤30.
∵x为整数,
∴x=28,29,30.
共有3种分派方案:
方案1,A地28台乙型掘井机,派往A地区2台甲型掘井机,派往B地2台乙型掘井机,派往B地18台甲型掘井机,
方案2,A地29台乙型掘井机,派往A地区1台甲型掘井机,派往B地1台乙型掘井机,派往B地19台甲型掘井机,
方案3,A地30台乙型掘井机,派往A地区0台甲型掘井机,派往B地0台乙型掘井机,派往B地20台甲型掘井机,
(3)∵y=20x+7400.
∴k=20>0,
∴y随x的增大而增大,
∴当x=30时,y最大为8000元.
∴该租赁公司采用方案3派送掘井机可以获得最大利润.
y=160x+180(30-x)+160(x-10)+120(30-x),
y=20x+7400.
∵
|
∴10≤x≤30;
(2)由题意,得
20x+7400≥7960,
解得:x≥28,
∵10≤x≤30;
∴28≤x≤30.
∵x为整数,
∴x=28,29,30.
共有3种分派方案:
方案1,A地28台乙型掘井机,派往A地区2台甲型掘井机,派往B地2台乙型掘井机,派往B地18台甲型掘井机,
方案2,A地29台乙型掘井机,派往A地区1台甲型掘井机,派往B地1台乙型掘井机,派往B地19台甲型掘井机,
方案3,A地30台乙型掘井机,派往A地区0台甲型掘井机,派往B地0台乙型掘井机,派往B地20台甲型掘井机,
(3)∵y=20x+7400.
∴k=20>0,
∴y随x的增大而增大,
∴当x=30时,y最大为8000元.
∴该租赁公司采用方案3派送掘井机可以获得最大利润.
点评:本题考查了列一元一次不等式组解实际问题的运用,一次函数的运用,方案设计的运用,一次函数的性质的运用,解答时求出一次函数的解析式是关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 如图,∠AOB=100°,OE是∠BOC的平分线,OD是∠AOC的平分线.求∠EOD的度数.
如图,∠AOB=100°,OE是∠BOC的平分线,OD是∠AOC的平分线.求∠EOD的度数.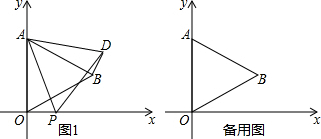
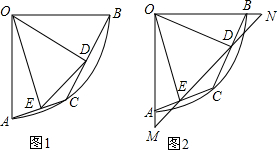 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E.
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合),OD⊥BC,OE⊥AC,垂足分别为D、E.