题目内容
如果ρ与ρ+2都是大于3的质数,那么请证明:6是ρ+1的约数.
考点:质数与合数,约数与倍数
专题:分类讨论
分析:由于ρ是大于3的质数,因此可分ρ<6和ρ>6两种情况讨论.当ρ<6时,显然ρ=5.则6是ρ+1的约数;当ρ>6时,由于ρ是大于3的质数,因此ρ是奇数,故有三种可能:ρ=6n+1或ρ=6n+3或ρ=6n+5,其中n为正整数.运用反证法可排除ρ=6n+1及ρ=6n+3两种情况,只有ρ=6n+5,此时ρ+1=6(n+1),则6是ρ+1的约数.
解答:解:(1)当ρ<6时,
∵ρ与ρ+2都是大于3的质数,
∴ρ=5.
∴ρ+1=6.
∴6是ρ+1的约数.
(2)当ρ>6时,
∵ρ是大于3的质数,
∴ρ是奇数.
∴ρ=6n+1或ρ=6n+3或ρ=6n+5,其中n为正整数.
①若ρ=6n+1,其中n为正整数,
则ρ+2=6n+3=3(2n+1)是3的倍数.
与条件“ρ+2是大于3的质数”矛盾,
故ρ≠6n+1.
②若ρ=6n+3,其中n为正整数,
则ρ=6n+3=3(2n+1)是3的倍数.
与条件“ρ是大于3的质数”矛盾,
故ρ≠6n+3.
所以ρ=6n+5,其中n为正整数.
此时ρ+1=6n+6=6(n+1),
则6是ρ+1的约数.
综上所述:如果ρ与ρ+2都是大于3的质数,那么6是ρ+1的约数.
∵ρ与ρ+2都是大于3的质数,
∴ρ=5.
∴ρ+1=6.
∴6是ρ+1的约数.
(2)当ρ>6时,
∵ρ是大于3的质数,
∴ρ是奇数.
∴ρ=6n+1或ρ=6n+3或ρ=6n+5,其中n为正整数.
①若ρ=6n+1,其中n为正整数,
则ρ+2=6n+3=3(2n+1)是3的倍数.
与条件“ρ+2是大于3的质数”矛盾,
故ρ≠6n+1.
②若ρ=6n+3,其中n为正整数,
则ρ=6n+3=3(2n+1)是3的倍数.
与条件“ρ是大于3的质数”矛盾,
故ρ≠6n+3.
所以ρ=6n+5,其中n为正整数.
此时ρ+1=6n+6=6(n+1),
则6是ρ+1的约数.
综上所述:如果ρ与ρ+2都是大于3的质数,那么6是ρ+1的约数.
点评:本题考查了质数、约数等知识,考查了分类讨论、排除法、反证法等思想方法,注重对能力的考查,是一道好题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
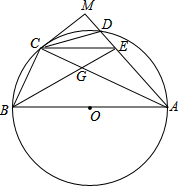 已知:如图,点D是以AB为直径的圆O上任意一点,且不与点A、B重合,点C是弧BD的中点,过C作CE∥AB,交AD或其延长线于E,连结B交AC于G.
已知:如图,点D是以AB为直径的圆O上任意一点,且不与点A、B重合,点C是弧BD的中点,过C作CE∥AB,交AD或其延长线于E,连结B交AC于G.