题目内容
7.平行四边形ABCD中,AB=10,AD=12,∠ABC=60°,E为边AD上一点,且AE=7,欲从平行四边形ABCD上剪下等腰△AEP(要求该等腰三角形的另一顶点P在平行四边形ABCD的一边上),请你求出等腰△AEP的面积.分析 分三种情形讨论:①当点P1在CD边上,EA=EP1时,②当点P1在BC边上,③当点P3在AB边上分别求解即可.
解答 解:如图,①当点P1在CD边上,EA=EP1时,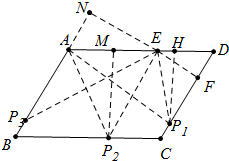 作P1H⊥AD,EF⊥CD垂足分别为H、F,
作P1H⊥AD,EF⊥CD垂足分别为H、F,
在RT△DEF中,∵∠EFD=90°,∠D=60°DE=5,
∴DF=$\frac{1}{2}$ED=$\frac{5}{2}$,EF=$\sqrt{D{E}^{2}-D{F}^{2}}$=$\frac{5\sqrt{3}}{2}$,
∵AE=EP1=7,
在RT△EFP1中,P1F=$\sqrt{E{{P}_{1}}^{2}-E{F}^{2}}$=$\frac{11}{2}$,
∴DP1=DF+P1F=8,
∵$\frac{1}{2}$•DE•P1H=$\frac{1}{2}$•DP1•EF,
∴P1H=4$\sqrt{3}$,
∴${S}_{△AE{P}_{1}}$=$\frac{1}{2}$•AE•P1H=14$\sqrt{3}$.
②当点P2在BC边上,P2A=P2E时,作P2M⊥AD垂足为M,${S}_{△{P}_{2}AE}$=$\frac{1}{2}$•AE•P2M=$\frac{1}{2}$×7×10×$\frac{\sqrt{3}}{2}$=$\frac{35\sqrt{3}}{2}$,
③当点P3在AB边上,AE=AP3时,作EN⊥BA于N.${S}_{△AE{P}_{3}}$=$\frac{1}{2}$AP3•EN=$\frac{1}{2}$×7×7×$\frac{\sqrt{3}}{2}$=$\frac{49\sqrt{3}}{4}$,
综上所述当△PAE是等腰三角形时面积为14$\sqrt{3}$或$\frac{35\sqrt{3}}{2}$或$\frac{49\sqrt{3}}{2}$.
点评 本题考查平行四边形的性质、等腰三角形的性质、勾股定理等知识解题的关键是学会分类讨论的方法,不能漏解,所以中考常考题型.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案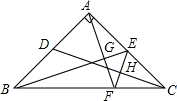 如图,在等腰三角形ABC中,∠BAC=90°,AB=AC,点D,E分别是AB,AC边上的中点,AF⊥BE交BC于点F,连接EF,交CD于点H,则下列结论:①∠FAE+∠EBF=45°;②$\frac{AG}{GE}$=$\frac{BG}{AG}$;③EF⊥CD;④CE=CF.其中结论正确的个数是( )
如图,在等腰三角形ABC中,∠BAC=90°,AB=AC,点D,E分别是AB,AC边上的中点,AF⊥BE交BC于点F,连接EF,交CD于点H,则下列结论:①∠FAE+∠EBF=45°;②$\frac{AG}{GE}$=$\frac{BG}{AG}$;③EF⊥CD;④CE=CF.其中结论正确的个数是( )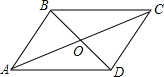 如图,?ABCD周长为100cm,AC与BD交于O,△OAB的周长与△OBC的周长的和为122cm,AC:BD=5:4,求AC与BD的长.
如图,?ABCD周长为100cm,AC与BD交于O,△OAB的周长与△OBC的周长的和为122cm,AC:BD=5:4,求AC与BD的长.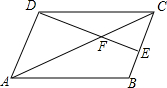 如图,四边形ABCD是平行四边形,E为BC边的中点,DE、AC相交于点F,若△CEF的面积为6,则四边形ABEF的面积为30.
如图,四边形ABCD是平行四边形,E为BC边的中点,DE、AC相交于点F,若△CEF的面积为6,则四边形ABEF的面积为30.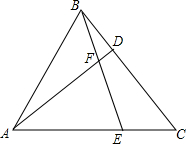 如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.
如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F. 已知:如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=8cm.求:
已知:如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=8cm.求: