题目内容
8.观察下列等式:①1+6×1=42-9×12;
②1+6×2=72-9×22;
③1+6×3=102-9×32;
…
根据上述规律解集下列问题:
(1)完成第四个等式:1+6×4=132-9×42;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
分析 (1)等式左边随序号在变化的只有第二个因数,并且是每个等式的序号数;等式右边第一个幂的底数,它是序号的3倍加1,第二个幂的底数显然也是序号数.
(2)将左边第二个因数用n表示,那么右边第一个底数是(3n+1),第二个底数为n,可完整表示出第n个等式.
解答 解:(1)等式左边随序号在变化的只有第二个因数,并且是每个等式的序号数;
等式右边第一个幂的底数,它是序号的3倍加1,第二个幂的底数显然也是序号数.
所以第4个等式为:1+6×4=(3×4+1)2-9×42,
即1+6×4=132-9×42;
答案为:4,13,4.
(2)第n个等式为:1+6n=(3n+1)2-9n2;
∵右边=(3n)2+2•(3n)•1+1-9n2
=9n2+6n+1-9n2
=6n+1=左边
∴1+6n=(3n+1)2-9n2成立.
点评 通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键是看清没个等式在变化的数与等式序号间的关系.

练习册系列答案
相关题目
19.已知$\left\{\begin{array}{l}{x+2y=-4m}\\{2x+y=2m+1}\end{array}\right.$,且x-y<0,则m的取值范围为( )
| A. | m$<\frac{1}{2}$ | B. | m$>\frac{1}{2}$ | C. | m$>-\frac{1}{2}$ | D. | m$<-\frac{1}{6}$ |
3.下列四个多项式,能因式分解的是( )
| A. | a2+b2 | B. | a2-a+2 | C. | a2+3b | D. | (x+y)2-4 |
 如图,AB=AD,DC=BC,∠B与∠D相等吗?为什么?
如图,AB=AD,DC=BC,∠B与∠D相等吗?为什么?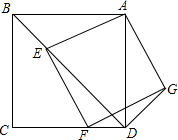 如图,已知正方形ABCD中,点E是对角线BD上一点,连接AE,以AE为边作正方形AEF0,使得点F在CD边上,连接DG,
如图,已知正方形ABCD中,点E是对角线BD上一点,连接AE,以AE为边作正方形AEF0,使得点F在CD边上,连接DG,