题目内容
11.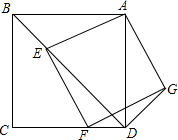 如图,已知正方形ABCD中,点E是对角线BD上一点,连接AE,以AE为边作正方形AEF0,使得点F在CD边上,连接DG,
如图,已知正方形ABCD中,点E是对角线BD上一点,连接AE,以AE为边作正方形AEF0,使得点F在CD边上,连接DG,(1)求证:BE=DG;
(2)若AB=4,BE=$\sqrt{2}$,求tan∠GFD的值.
分析 (1)由正方形的性质得出AB=AD,∠BAD=∠ADC=90°,∠ABD=45°,AE=AG,∠EAG=90°,得出∠BAE=∠DAG,由SAS证明△ABE≌△ADG,得出∠ADG=∠ABD=45°,BE=DG;
(2)作GH⊥CD交CD延长线于点H,GT⊥AD于点I,证出四边形DHGI为正方形,得出DH=HG=1,AI=3,由勾股定理求出AG,得出FG,由勾股定理求出FH,即可得出结果.
解答 (1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=∠ADC=90°,∠ABD=45°,
∵四边形AEFG为正方形,
∴AE=AG,∠EAG=90°,
∴∠BAE=∠DAG,
在△ABE和△ADG中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAG}\\{AE=AG}\end{array}\right.$,
∴△ABE≌△ADG(SAS),
∴∠ADG=∠ABD=45°,BE=DG;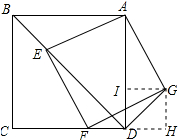
(2)解:作GH⊥CD交CD延长线于点H,GT⊥AD于点I,如图所示:
∵∠ADC=∠ADH=90°,
∴四边形DHGI为矩形,
∵∠ADG=45°,
∴∠GDH=45°,
∴GI=GH,
∴四边形DHGI为正方形,
∵DG=BE=$\sqrt{2}$,
∴DH=HG=1,
∴ID=IG=1,
∵AB=4,
∴AI=4-1=3,
∴AG=$\sqrt{A{I}^{2}+I{G}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∴FG=$\sqrt{10}$,FH=$\sqrt{F{G}^{2}-H{G}^{2}}$=$\sqrt{(\sqrt{10})^{2}-{1}^{2}}$=3,
∴tan∠GFD=$\frac{HG}{FH}$=$\frac{1}{3}$.
点评 本题考查了正方形的性质与判定、全等三角形的判定与性质、勾股定理、三角函数等知识;本题综合性强,有一定难度,特别是(2)中,需要证明四边形是正方形和多次运用勾股定理才能得出结果.

 如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )| A. | 0<x<1 | B. | -1<x<0 | C. | x<0或x>1 | D. | x<-1或x>0 |
 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),且点A的坐标是(-1,0),与y轴交于点C,点C的坐标是(0,3),连接AC.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于A、B两点(点A在点B的左侧),且点A的坐标是(-1,0),与y轴交于点C,点C的坐标是(0,3),连接AC. 如图,已知△ABC,点D在边BC上,点E在边AC上,点F在边AB上,且DE∥D1E1,EF∥E1F1,DF∥D1F1.求证:S△DEF•S△D1E1F1=S2△ABC.
如图,已知△ABC,点D在边BC上,点E在边AC上,点F在边AB上,且DE∥D1E1,EF∥E1F1,DF∥D1F1.求证:S△DEF•S△D1E1F1=S2△ABC. 如图,在直角坐标系中,点A(8,0),点B(0,4),点C(-4,-4),连接BC与x轴相交于点D,连接AC与y轴相交于点E,连接DE.
如图,在直角坐标系中,点A(8,0),点B(0,4),点C(-4,-4),连接BC与x轴相交于点D,连接AC与y轴相交于点E,连接DE.