题目内容
16.先化简,再求值:$\frac{a-b}{a}÷(a-\frac{2ab-{b}^{2}}{a})$,其中a=6sin30°+cos45°,b=$\sqrt{3}$tan60°.分析 先把括号内通分,再把分子分解因式后把除法运算化为乘法运算得到原式=$\frac{1}{a-b}$,然后根据特殊角的三角函数值计算出a和b的值,再把a和b的值代入$\frac{1}{a-b}$中计算即可.
解答 解:原式=$\frac{a-b}{a}$÷$\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{a-b}{a}$•$\frac{a}{(a-b)^{2}}$
=$\frac{1}{a-b}$,
∵a=6sin30°+cos45°=6×$\frac{1}{2}$+$\frac{\sqrt{2}}{2}$=3+$\frac{\sqrt{2}}{2}$,b=$\sqrt{3}$tan60°=$\sqrt{3}$×$\sqrt{3}$=3,
∴原式=$\frac{1}{3+\frac{\sqrt{2}}{2}-3}$=$\sqrt{2}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了特殊角的三角函数值.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
4.袋中装有大小一样的白球和黑球各3个,从中任取2个球,则两个均为黑球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
11.聪聪的文件夹里放了大小相同的试卷共12页,其中语文6页,数学4页,英语2页,他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
1.与-3的积为1的数是( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -3 |
6. 如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
 如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )
如图,二次函数y=ax2+c的图象与一次函数y=kx+c的图象在第一象限的交点为A,点A的横坐标为1,则关于x的不等式ax2-kx<0的解集为( )| A. | 0<x<1 | B. | -1<x<0 | C. | x<0或x>1 | D. | x<-1或x>0 |
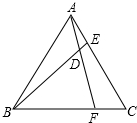 已知△ABC为等边三角形,点E、F分别在边AC、BC上,且AE=CF,AF与BE相交于点D.
已知△ABC为等边三角形,点E、F分别在边AC、BC上,且AE=CF,AF与BE相交于点D.