题目内容
15.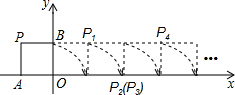 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转48次,点P依次落在点P1,P2,P3,P4,…,P48的位置,则P48的坐标是(47,1).
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转48次,点P依次落在点P1,P2,P3,P4,…,P48的位置,则P48的坐标是(47,1).
分析 首先看清P点的坐标为(-1,1),然后将正方形看成一个整体,反转四次就可以回到原来的相对位置,根据这规律就可以求出P48的坐标.
解答 解:∵P=(-1,1)
正方形有四条边,翻转4次后,正方形等于沿x轴正方向平移4个单位边长的距离,
P4=(-1+1×4,1)=(3,1),
翻转4N次后,P点落在(-1+4N,1)上,
P48=(47,1),
P48的横坐标为47.
故答案为:(47,1).
点评 题目考查了点的坐标的规律性,根据规律找出相应点的坐标即可.题目相对较简单,但是可以考察学生的分析问题解决问题的能力.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
3.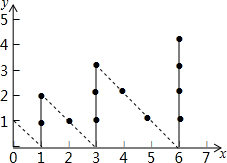 如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )
如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )
 如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )
如图,一个粒子从原点出发,每分钟移动一次,依次运动到(0,1)→(1,0)→(1,1)→(1,2)→(2,1)→…,则2015分钟时粒子所在点的横坐标为( )| A. | 886 | B. | 903 | C. | 946 | D. | 990 |
7.下列方程中是一元二次方程的是( )
| A. | (x-1)(3+x)=5 | B. | x2+$\frac{1}{x}$-$\frac{9}{2}$=0 | C. | y2+2x+4=0 | D. | 4x2=(2x-1)2 |
5.某公司生产、销售A种产品,它的成本是6元/件,售价是8元/件,年销售量为5万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,若每年投入的广告费是x万元,则产品的年销售量将是原来年销售量的y倍,且y与x之间满足二次函数关系,y与x的部分对应值如下表:
(1)求y与x之间的函数关系式(不要求写出自变量的取值范围).
(2)如果把利润看作是销售总额减去成本费和广告费,试求出年利润W(万元)与广告费x(万元)之间的函数关系式,并计算每年投入的广告费是多少万元时获得的年利润最大?
(3)如果公司希望年利润W(万元)不低于14万元,请你帮公司确定广告费的范围.
| x(万元) | 0 | 1 | 2 | … |
| y | 1 | 1.5 | 1.8 | … |
(2)如果把利润看作是销售总额减去成本费和广告费,试求出年利润W(万元)与广告费x(万元)之间的函数关系式,并计算每年投入的广告费是多少万元时获得的年利润最大?
(3)如果公司希望年利润W(万元)不低于14万元,请你帮公司确定广告费的范围.
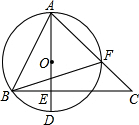 变式:如图,AD是⊙O的直径,AD⊥BC,△ABF与△ACB相似吗?
变式:如图,AD是⊙O的直径,AD⊥BC,△ABF与△ACB相似吗?