��Ŀ����
5��ij��˾����������A�ֲ�Ʒ�����ijɱ���6Ԫ/�����ۼ���8Ԫ/������������Ϊ5�����Ϊ�˻�ø��õ�Ч�棬��˾���ó�һ�����ʽ�����棬���ݾ��飬��ÿ��Ͷ��Ĺ�����x��Ԫ�����Ʒ��������������ԭ������������y������y��x֮��������κ�����ϵ��y��x�IJ��ֶ�Ӧֵ���±���| x����Ԫ�� | 0 | 1 | 2 | �� |
| y | 1 | 1.5 | 1.8 | �� |
��2��������������������ܶ��ȥ�ɱ��Ѻ��ѣ������������W����Ԫ�������x����Ԫ��֮��ĺ�����ϵʽ��������ÿ��Ͷ��Ĺ����Ƕ�����Ԫʱ��õ����������
��3�������˾ϣ��������W����Ԫ��������14��Ԫ������﹫˾ȷ�����ѵķ�Χ��
���� ��1�����κ����Ľ���ʽΪy=ax2+bx+c�����ñ������ݣ��������y��x֮��ĺ�����ϵʽ��
��2�������������������ܶ��ȥ�ɱ��Ѻ��ѣ��ɵý��ۣ�
��3�������䷽�������x��ȡֵ��Χ��������ֵ��
��� �⣺��1������κ����Ľ���ʽΪy=ax2+bx+c��
�ɹ�ϵ������$\left\{\begin{array}{l}{c=1}\\{a+b+c=1.5}\\{4a+2b+c=1.8}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{10}}\\{b=\frac{3}{5}}\\{c=1}\end{array}\right.$��
�ຯ���Ľ���ʽΪy=-$\frac{1}{10}$x2+$\frac{3}{5}$x+1��
��2���������⣬��W=5y��8-6��-x=-x2+5x+10
��3��W=-x2+5x+10=-��x-$\frac{5}{2}$��2+$\frac{65}{4}$��
��1��x��4��
�൱1��x��2.5ʱ��S��x�����������
�ʵ������Ϊ1��2.5��Ԫ֮�䣬��˾��õ�����������ѵ����������
�൱1��x��4ʱ����������14��Ԫ��
���� ���⿼����Ƕ��κ�����Ӧ�ã��漰������ģ�͵Ľ������䷽�������õ�֪ʶ������ѧ�������������������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
10�����������������⣺
��1��������֣���x��-1��ʼ����ʱ��Ԥ����һ��������ֵ�ȵ���16��
��2���������һ��������ϵ����1�Ķ��κ�����ʹ�õ�x=4ʱ������ֵΪ16������ĺ�������ʽ��ʲô��
| x | �� | -1 | 0 | 1 | 2 | �� |
| y1=2x+3 | �� | 1 | 3 | 5 | 7 | �� |
| y2=x2 | �� | 1 | 0 | 1 | 4 | �� |
��2���������һ��������ϵ����1�Ķ��κ�����ʹ�õ�x=4ʱ������ֵΪ16������ĺ�������ʽ��ʲô��
15����������ͼ��һ�����Ƶ��ǣ�������
| A�� | �������� | B�� | �������������� | C�� | ��������� | D�� | ���������� |
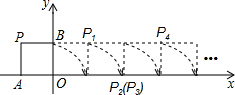 ��ͼ�����߳�Ϊ1��������OAPB��x��������������ת48�Σ���P�������ڵ�P1��P2��P3��P4������P48��λ�ã���P48�������ǣ�47��1����
��ͼ�����߳�Ϊ1��������OAPB��x��������������ת48�Σ���P�������ڵ�P1��P2��P3��P4������P48��λ�ã���P48�������ǣ�47��1����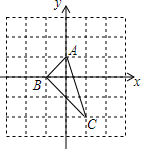 ��ͼ����6��6�������������У�ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ��������㣬��A��B��C��O���ڸ���ϣ���ͼ��ʾ����ƽ��ֱ������ϵ����Ҫ��������л�ͼ��
��ͼ����6��6�������������У�ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ��������㣬��A��B��C��O���ڸ���ϣ���ͼ��ʾ����ƽ��ֱ������ϵ����Ҫ��������л�ͼ��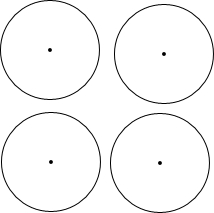 ��ͼ����O�İ뾶Ϊ3cm�����������Բ�ֳ����������ȵ������֣���������������ַ�����Ҫ��1����ͼ�εķָ�ʾ��ͼ��2��ͼ�б����ؼ�����Ҫ�����ݣ�3���мļ���˵�����̣�
��ͼ����O�İ뾶Ϊ3cm�����������Բ�ֳ����������ȵ������֣���������������ַ�����Ҫ��1����ͼ�εķָ�ʾ��ͼ��2��ͼ�б����ؼ�����Ҫ�����ݣ�3���мļ���˵�����̣�