题目内容
4.某商场销售一批进价为120元的名牌衬衫,平均每天可销售20件,每件可盈利40元.经调查发现,在一定范围内,衬衫的单价每降1元,每天就可多售出2件衬衫.这种衬衫的单价应降价多少元?才能使商场通过销售这批衬衫平均每天盈利1200元.分析 设衬衫的单价应下降x元.则每天可售出(20+2x)件,每件盈利(40-x)元.再根据相等关系:每天的获利=每天售出的件数×每件的盈利;列方程求解即可.
解答 解:设这种衬衫的单价应降价x元,
根据题意,得 (20+2x) (40-x)=1200,
解得:x1=10,x2=20.
答:这种衬衫的单价应降价10元或20元,才能使商场平均每天盈利1200元.
点评 此题考查了一元二次方程的应用,找到题目的相等关系:每天的获利=每天售出的件数×每件的盈利是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.对于一元二次方程ax2+bx+c=0 (a≠0),下列说法中错误的是( )
| A. | 当a>0,c<0时,方程一定有实数根 | |
| B. | 当c=0时,方程至少有一个根为0 | |
| C. | 当a>0,b=0,c<0时,方程的两根一定互为相反数 | |
| D. | 当abc<0时,方程的两个根同号,当abc>0时,方程的两个根异号 |
 如图,AB是⊙O的直径,点C在⊙O上,∠AOC=40°,D是$\widehat{BC}$的中点,求∠ACD的度数.
如图,AB是⊙O的直径,点C在⊙O上,∠AOC=40°,D是$\widehat{BC}$的中点,求∠ACD的度数.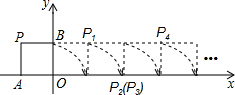 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转48次,点P依次落在点P1,P2,P3,P4,…,P48的位置,则P48的坐标是(47,1).
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转48次,点P依次落在点P1,P2,P3,P4,…,P48的位置,则P48的坐标是(47,1).



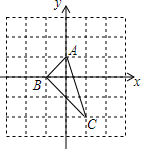 如图,在6×6的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,点A、B、C、O都在格点上,如图所示建立平面直角坐标系,按要求完成下列画图.
如图,在6×6的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,点A、B、C、O都在格点上,如图所示建立平面直角坐标系,按要求完成下列画图.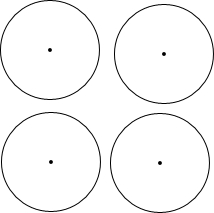 如图,⊙O的半径为3cm,现准备将这个圆分成三个面积相等的三部分.请你设计至少四种方案(要求:1.有图形的分割示意图;2.图中标明关键而必要的数据;3.有简单的计算说明过程)
如图,⊙O的半径为3cm,现准备将这个圆分成三个面积相等的三部分.请你设计至少四种方案(要求:1.有图形的分割示意图;2.图中标明关键而必要的数据;3.有简单的计算说明过程)