题目内容
17. 如图,在△BAD中,∠BAD=90°,延长斜边BD到点C,使DC=$\frac{1}{2}BD$,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值$\frac{1}{5}$.
如图,在△BAD中,∠BAD=90°,延长斜边BD到点C,使DC=$\frac{1}{2}BD$,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值$\frac{1}{5}$.
分析 延长AD,过点C作CE⊥AD,垂足为E,设AD=5x,则AB=3x,再证出△CDE∽△BDA,得出$\frac{CE}{AB}$=$\frac{DE}{AD}$=$\frac{CD}{BD}$=$\frac{1}{2}$,设CE=$\frac{3}{2}$x,DE=$\frac{5}{2}$x,求出AE=$\frac{15}{2}$x,最后根据tan∠CAD=$\frac{EC}{AE}$代入计算即可.
解答  解:如图,延长AD,过点C作CE⊥AD,垂足为E,
解:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=$\frac{5}{3}$,
∴$\frac{AD}{AB}$=$\frac{5}{3}$,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴$\frac{CE}{AB}$=$\frac{DE}{AD}$=$\frac{CD}{BD}$=$\frac{1}{2}$,
∴CE=$\frac{3}{2}$x,DE=$\frac{5}{2}$x,
∴AE=$\frac{15}{2}$x,
∴tan∠CAD=$\frac{EC}{AE}$=$\frac{1}{5}$,
故答案为:$\frac{1}{5}$.
点评 本题考查了锐角三角函数的定义,相似三角形的判定和性质以及直角三角形的性质,是基础知识要熟练掌握,解题的关键是:正确添加辅助线,将∠CAD放在直角三角形中.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
12.对于二次函数y=(x-2)2+2的图象,下列说法正确的是( )
| A. | 开口向下 | B. | 对称轴是x=-2 | C. | 顶点坐标是(-2,2) | D. | 与x轴无交点 |
2.已知|n+2|+(5m-3)2=0,则关于x的方程10mx+4=3x+n的解是x=( )
| A. | 2 | B. | -2 | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
7.若点A(-1,a),B(2,b),C(3,c)在抛物线y=x2上,则下列结论正确的是( )
| A. | a<c<b | B. | b<a<c | C. | c<b<a | D. | a<b<c |
 如图,已知∠ABC=90°,D是直线AB上的点,AD=BC,如图,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF.
如图,已知∠ABC=90°,D是直线AB上的点,AD=BC,如图,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF. 如图,线段AB=1cm,延长AB到C,使得BC=$\frac{3}{2}$AB,反向延长AB到D,使得BD=2BC,在线段CD上有一点P,且AP=2cm.
如图,线段AB=1cm,延长AB到C,使得BC=$\frac{3}{2}$AB,反向延长AB到D,使得BD=2BC,在线段CD上有一点P,且AP=2cm.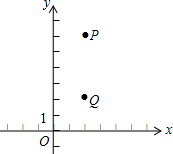 在平面直角坐标系中,P点坐标为(2,6),Q点坐标为(2,2),点M为y轴上的动点.
在平面直角坐标系中,P点坐标为(2,6),Q点坐标为(2,2),点M为y轴上的动点.