题目内容
6.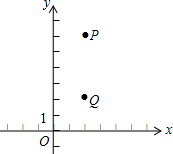 在平面直角坐标系中,P点坐标为(2,6),Q点坐标为(2,2),点M为y轴上的动点.
在平面直角坐标系中,P点坐标为(2,6),Q点坐标为(2,2),点M为y轴上的动点.(1)在平面直角坐标系内画出当△PMQ的周长取最小值时点M的位置.(保留作图痕迹)
(2)写出点M的坐标(0,4).
分析 (1)作点Q关于y轴的对称点Q′,连接PQ交y轴与点M,点M即为所求;
(2)设直线Q′P的解析式为y=kx+b,将点Q′、点P的坐标代入可求得b=4,从而可得到点M的坐标.
解答 解:(1)如图所示:
(2)设直线Q′P的解析式为y=kx+b,将点Q′、点P的坐标代入得:$\left\{\begin{array}{l}{2k+b=6}\\{-2k+b=2}\end{array}\right.$.
解得:b=4.
故点M的坐标为(0,4).
点评 本题主要考查的是轴对称路径最短问题,明确当点P、M、Q′在一条直线上时,△PMQ的周长取最小值是解题的关键.

练习册系列答案
相关题目
18.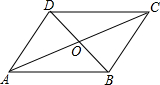 如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )
如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )
 如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )
如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )| A. | $\overrightarrow{OA}$ | B. | $\overrightarrow{OB}$ | C. | $\overrightarrow{OC}$ | D. | $\overrightarrow{OD}$ |
15.若(m-2)${x}^{{m}^{2}-2}$-x+1=0是一元二次方程,则m的值为( )
| A. | ±2 | B. | 2 | C. | -2 | D. | 以上结论都不对 |
16.tan30°=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |

 如图,在△BAD中,∠BAD=90°,延长斜边BD到点C,使DC=$\frac{1}{2}BD$,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值$\frac{1}{5}$.
如图,在△BAD中,∠BAD=90°,延长斜边BD到点C,使DC=$\frac{1}{2}BD$,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值$\frac{1}{5}$.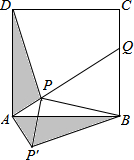 如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.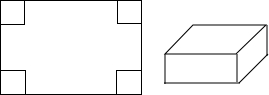 如图是以长为120cm,宽为80cm的长方形硬纸,在它的四个角处各剪去一个边长为20cm的正方形后,将其折叠成如图所示的无盖的长方体,则这个长方体的体积为64000立方厘米.
如图是以长为120cm,宽为80cm的长方形硬纸,在它的四个角处各剪去一个边长为20cm的正方形后,将其折叠成如图所示的无盖的长方体,则这个长方体的体积为64000立方厘米.