题目内容
7.若点A(-1,a),B(2,b),C(3,c)在抛物线y=x2上,则下列结论正确的是( )| A. | a<c<b | B. | b<a<c | C. | c<b<a | D. | a<b<c |
分析 根据二次函数的性质,通过三点与对称轴距离的远近来比较函数值的大小.
解答 解:由抛物线y=x2可知对称轴为y轴,
∵抛物线开口向上,|-1|<|2|<|3|,
∴a<b<c.
故选D.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
相关题目
18.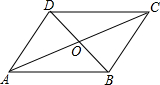 如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )
如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )
 如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )
如图,?ABCD对角线AC与BD相交于点O,如果$\overrightarrow{AB}$=$\overrightarrow{m}$,$\overrightarrow{AD}$=$\overrightarrow{n}$,那么下列选项中,与向量$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)相等的向量是( )| A. | $\overrightarrow{OA}$ | B. | $\overrightarrow{OB}$ | C. | $\overrightarrow{OC}$ | D. | $\overrightarrow{OD}$ |
15.若(m-2)${x}^{{m}^{2}-2}$-x+1=0是一元二次方程,则m的值为( )
| A. | ±2 | B. | 2 | C. | -2 | D. | 以上结论都不对 |
16.tan30°=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
17.若一元二次方程(1-2k)x2+8x-6=0没有实数根,那么k的最小值是( )
| A. | 2 | B. | 0 | C. | 1 | D. | 3 |
 如图,在△BAD中,∠BAD=90°,延长斜边BD到点C,使DC=$\frac{1}{2}BD$,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值$\frac{1}{5}$.
如图,在△BAD中,∠BAD=90°,延长斜边BD到点C,使DC=$\frac{1}{2}BD$,连接AC,若tanB=$\frac{5}{3}$,则tan∠CAD的值$\frac{1}{5}$.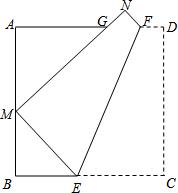 如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:
如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明: