题目内容
如图①,先把一矩形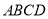 纸片上下对折,设折痕为
纸片上下对折,设折痕为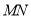 ;如图②,再把
;如图②,再把
点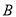 叠在折痕线
叠在折痕线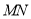 上,得到
上,得到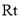
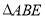 .过
.过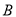 点作
点作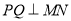 ,分别交
,分别交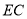 、
、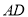 于点
于点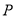 、
、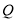 .
.
(1)求证: 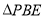 ∽
∽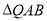 ;
;
(2)在图②中,如果沿直线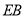 再次折叠纸片,点
再次折叠纸片,点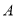 能否叠在直线
能否叠在直线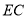 上?请说明理由;
上?请说明理由;
(3)在(2)的条件下,若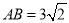 ,求
,求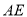 的长度.
的长度.
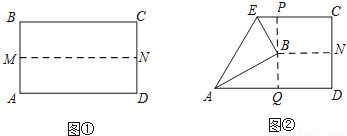
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y,的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
(1)根据上表填空:
①抛物线与x轴的交点坐标是_________和_________;
②抛物线经过点(-3,_________);
(2)试确定抛物线y=ax2+bx+c的解析式.
(1)①(-2,0),(1,0);②8;(2)所求抛物线解析式为y=2x2+2x-4. 【解析】试题分析: (1)①根据表格中函数值y=0即可得到与x轴的交点坐标; ②观察表格可知抛物线的对称轴为x=,由此可知(2,8)与(-3,8)关于对称轴对称,从而可得; (2)依题意设抛物线解析式为y=a(x+2)(x-1),代入点(0,-4)即可求得. 试题解析:(1)①观察表格可...

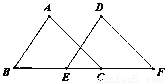
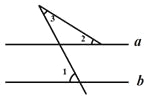
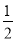 ∠B=
∠B=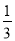 ∠C,则此三角形是( )
∠C,则此三角形是( )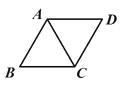
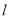 和双曲线
和双曲线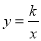 (
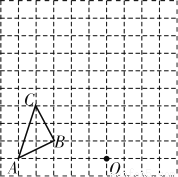
(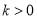 )交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴 作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则有( )
)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴 作垂线,垂足分别为C、D、E,连接OA、OB、OP,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则有( )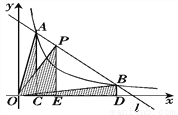
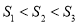 B.
B. 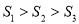 C.
C. 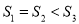 D.
D. 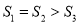
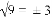 B. (m2)3=m5 C. a2•a3=a5 D. (x+y)2=x2+y2
B. (m2)3=m5 C. a2•a3=a5 D. (x+y)2=x2+y2