题目内容

16．（1）（-2）-1-|-$\sqrt{8}$|+（3.14-π）0+4cos45°
（2）已知x2-2x-7=0，求（x-2）2+（x+3）（x-3）的值．

分析 （1）原式利用零指数幂、负整数指数幂法则，绝对值的代数意义，以及特殊角的三角函数值计算即可得到结果；
（2）原式利用完全平方公式，平方差公式化简，去括号整理后，将已知等式变形后代入计算即可求出值．

解答 解：（1）原式=-$\frac{1}{2}$-2$\sqrt{2}$+1+2$\sqrt{2}$=$\frac{1}{2}$；
（2）原式=x2-4x+4+x2-9=2x2-4x-5=2（x2-2x）-5，
∵x2-2x-7=0，即x2-2x=7，
∴原式=14-5=9．

点评 此题考查了整式的混合运算-化简求值，以及实数的运算，熟练掌握公式及运算法则是解本题的关键．

练习册系列答案
相关题目
9．一元二次方程x2-6x-6=0配方后化为（　　）
A．（x-3）2=15B．（x-3）2=3C．（x+3）2=15D．（x+3）2=3
7．在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下两幅统计图．请根据相关信息，解答下列问题：

（1）扇形统计图中，初赛成绩为1.65m所在扇形图形的圆心角为54°；
（2）补全条形统计图；
（3）这组初赛成绩的中位数是1.60m；
（4）根据这组初赛成绩确定8人进入复赛，那么初赛成绩为1.60m的运动员杨强能否进入复赛？为什么？
4．设数据：1，2，3，4，5的方差为S12，数据：11，12，13，14，15的方差为S22，则S12=S22．（填：“＞”、“＜”或“=”）．
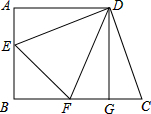11．如图，正方形ABCD中，边长为12，DE⊥DC交AB于点E，DF平分∠EDC交BC于点F，连接EF．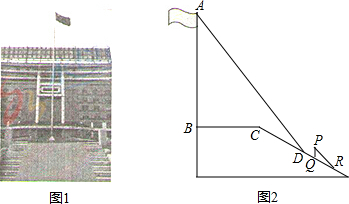
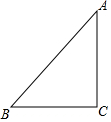（1）求证：EF=CF；
（2）当$\frac{AE}{AD}$=$\frac{1}{3}$时，求EF的长．
1．某中学广场上有旗杆如图1所示，在学习解直角三角形以后，数学兴趣小组测量了旗杆的长度．如图2，在某一时刻，光线与水平面的夹角为72°，旗杆AB的影子一部分落在平台上，另一部分落在斜坡上，测得落在平台上的影长BC为4米，落在斜坡上的影长CD为3米，AB⊥BC，同一时刻，若1米的竖立标杆PQ在斜坡上的影长QR为2米，求旗杆AB的长度．（结果精确到0.1米．参考数据：sin72°≈0.95，cos72°≈0.31，tan72°≈3.08）．
8．在四张背面完全相同的纸牌A、B、C、D中，其中正面分别画有四个不同的几何图形（如图），小华将这4张纸牌背面朝上洗匀后摸出一张（不放回），再从余下的3张纸牌中摸出一张．
（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌可用A、B、C、D表示）；
（2）求摸出两张纸牌牌面上所画几何图形，既是轴对称图形又是中心对称图形的概率．
5．如图，已知△ABC中，∠C=90°，AC=BC=$\sqrt{2}$，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B．
（1）请你在图中把图补画完整；
（2）求C′B的长．
6．如图，我区某中学开展“健康运动”的活动，决定开设“A：乒乓球，B：拔河，C：跳绳，D：篮球”四种运动项目，为了解学生最喜欢哪一种运动项目（每位同学均只选择一项），随机抽取了九年级部分学生，根据调查结果绘制成如图的统计图：
（1）本次共调查了200学生，其中最喜欢跳绳运动项目的学生数为40人；在扇形图中，最喜欢拔河的对应扇形的圆心角大小是54度；
（2）根据以上统计分析，在这四种“健康运动”项目中，学生最喜欢的运动项目是什么？并估计该校1200名学生中喜欢此项目的学生人数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网