题目内容
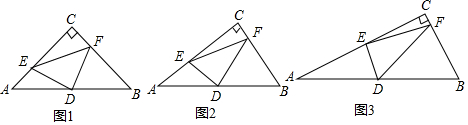
1.某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的长度.如图2,在某一时刻,光线与水平面的夹角为72°,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,若1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆AB的长度.(结果精确到0.1米.参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08).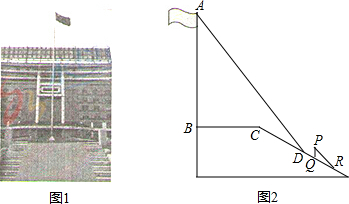
分析 如图作CM∥AB交AD于M,MN⊥AB于N,根据 $\frac{CM}{CD}$=$\frac{PQ}{QR}$,求出CM,在RT△AMN中利用tan72°=$\frac{AN}{MN}$,求出AN即可解决问题.
解答 解:如图,作CM∥AB交AD于点M,MN⊥AB于点N.
由题意$\frac{CM}{CD}$=$\frac{PQ}{QR}$,即$\frac{CM}{3}$=$\frac{1}{2}$,
∴CM=(米),
在Rt△AMN中,∵∠ANM=90°,MN=BC=4米,∠AMN=72°,
∴tan 72°=$\frac{AN}{MN}$,
∴AN=MN•tan 72°≈4×3.08≈12.3(米).
∵MN∥BC,AB∥CM,
∴四边形MNBC是平行四边形,
∴BN=CM=米,
∴AB=AN+BN=13.8米.
点评 本题考查解直角三角形、三角函数,影长等知识,解题的关键是正确添加辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
14.已知一次函数y=kx-m-2x的图象与y轴的负半轴相交,且函数值y随自变量x的增大而减小,则下列结论正确的是( )
| A. | k<2,m>0 | B. | k<2,m<0 | C. | k>2,m>0 | D. | k<0,m<0 |

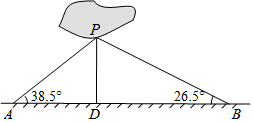 如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)
如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)