题目内容
11.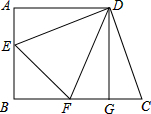 如图,正方形ABCD中,边长为12,DE⊥DC交AB于点E,DF平分∠EDC交BC于点F,连接EF.
如图,正方形ABCD中,边长为12,DE⊥DC交AB于点E,DF平分∠EDC交BC于点F,连接EF.(1)求证:EF=CF;
(2)当$\frac{AE}{AD}$=$\frac{1}{3}$时,求EF的长.
分析 (1)根据正方形的性质和全等三角形的判定和性质证明即可;
(2)设EF=x,根据勾股定理解答即可.
解答 (1)证明:∵正方形ABGD,
又∵DE⊥DC,
∴∠ADE+∠EDG=90°=∠GDC+∠EDG,
∴∠ADE=∠GDC.
又∵∠A=∠DGC,
且AD=GD,
在△ADE与△GDC中,
$\left\{\begin{array}{l}{∠ADE=∠GDC}\\{AD=DG}\\{∠A=∠DGC}\end{array}\right.$,
∴△ADE≌△GDC(ASA).
∴DE=DC,且AE=GC.
在△EDF和△CDF中,
$\left\{\begin{array}{l}{DE=DC}\\{∠EDF=∠D=CDF}\\{DF=DF}\end{array}\right.$,
∴△EDF≌△CDF(SAS).
∴EF=CF;
(2)解:∵$\frac{AE}{AD}$=$\frac{1}{3}$,
∴AE=GC=4.
设EF=x,则BF=16-CF=16-x,BE=12-4=8.
由勾股定理,得x2=(16-x)2+82.
解之,得x=10,
即EF=10.
点评 此题考查正方形的性质,关键是根据正方形的性质和全等三角形的判定和性质解答.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
4.下列四个数:-3,-$\sqrt{3}$,-π,-1,其中最小的数是( )
| A. | -π | B. | -3 | C. | -1 | D. | -$\sqrt{3}$ |
6.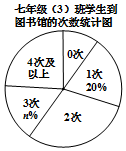 为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:
为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:
(1)求图表中m,n的值;
(2)该年级学生共有300人,估计这周到图书馆的次数为“4次及以上”的学生大约有多少人?
七年级(3)班学生到图书馆的次数统计表
 为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:
为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:(1)求图表中m,n的值;
(2)该年级学生共有300人,估计这周到图书馆的次数为“4次及以上”的学生大约有多少人?
七年级(3)班学生到图书馆的次数统计表
| 到图书馆的 次数 | 0次 | 1次 | 2次 | 3次 | 4次及 以上 |
| 人数 | 5 | 10 | m | 8 | 12 |
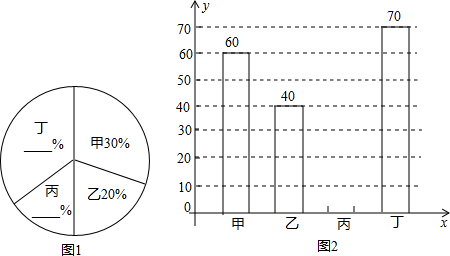
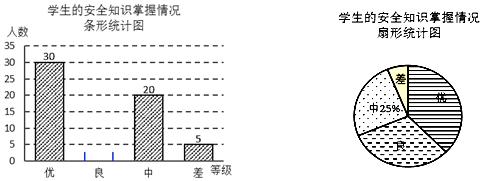
20.某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣,利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查.
根据调查结果绘制出了如下两幅尚不完整的统计图.
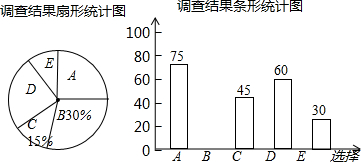
根据以上信息解答下列问题:
(1)这次接受调查的总人数为300人;
(2)在扇形统计图中,“A”所在扇形的圆心角的度数为90°;
(3)补全条形统计图;
(4)若该市有1000万人,请你估计选D的总人数.
| 造成医患关系紧张的原因(单选) A.药价高 B.检测项目太多且收费太高 C.住院报销比例低 D.医疗费与个人收入不相称 E.其他 |

根据以上信息解答下列问题:
(1)这次接受调查的总人数为300人;
(2)在扇形统计图中,“A”所在扇形的圆心角的度数为90°;
(3)补全条形统计图;
(4)若该市有1000万人,请你估计选D的总人数.
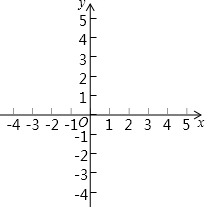 在平面直角坐标系xOy,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2)
在平面直角坐标系xOy,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2)