题目内容
9.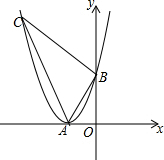 如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.
如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.(1)求抛物线的解析式及直线AC的解析式;
(2)△ABC的面积为5.
分析 (1)根据顶点的特点得出4ac=b2,结合ac=b求得b=4,根据b的坐标求得c=4,进而求得a=1,从而求得二次函数的解析式,根据解析式求得顶点A的坐标,设出直线AC的解析式,代入A的坐标,根据待定系数法即可求得直线的解析式;
(2)联立方程求得C的坐标,然后根据梯形的面积减去两个三角形的面积求得即可.
解答 解:(1)∵顶点A在轴上,
∴$\frac{4ac-{b}^{2}}{4a}$=0,
∴4ac=b2
∵ac=b.
∴4b=b2,
∵b≠0,
∴b=4,
∵抛物线y=ax2+bx+c与y轴的交点为B(0,4),
∴c=4,
∴a=1,
∴抛物线的解析式为y=x2+4x+4,;
∵y=x2+4x+4=(x+2)2,
∴A(-2,0),
∵平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.
∴设直线AC为y=-3x+n,
把(-2,0)代入得,6+n=0,
∴n=-6,
∴直线AC的解析式为y=-3x-6;
(2)解$\left\{\begin{array}{l}{y=-3x-6}\\{y={x}^{2}+4x+4}\end{array}\right.$得$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-5}\\{y=9}\end{array}\right.$,
∴C(-5,9),
∴S△ABC=$\frac{1}{2}$(4+9)×5-$\frac{1}{2}$(5-2)×9-$\frac{1}{2}$×2×4=5.
故答案为5.
点评 本题考查了二次函数的性质,根据顶点坐标求得b的值是解题的关键.

练习册系列答案
相关题目
4. 近段时间,我国大部分城市持续出现雾霾天气.某市记者为了“了解雾霾天气的主要原因”,随机调查了该市部分市民,并对调查结果进行整理.绘制了如下尚不完全的统计图表.
近段时间,我国大部分城市持续出现雾霾天气.某市记者为了“了解雾霾天气的主要原因”,随机调查了该市部分市民,并对调查结果进行整理.绘制了如下尚不完全的统计图表.
请根据图表中提的信息解答下列问题:
(1)填空:m=40,n=100,扇形统计图中扇形E组圆心角的度数为54°;
(2)若该市人口约有100万人,请你估计其中持“D组”观点的市民人数.
 近段时间,我国大部分城市持续出现雾霾天气.某市记者为了“了解雾霾天气的主要原因”,随机调查了该市部分市民,并对调查结果进行整理.绘制了如下尚不完全的统计图表.
近段时间,我国大部分城市持续出现雾霾天气.某市记者为了“了解雾霾天气的主要原因”,随机调查了该市部分市民,并对调查结果进行整理.绘制了如下尚不完全的统计图表.| 组别 | 观点 | 頻数(人数) |
| A | 大气气压低,空气不流动 | 80 |
| B | 地面灰尘大,空气湿度低 | m |
| C | 汽车尾气排放 | n |
| D | 工厂造成的污染 | 120 |
| E | 其他 | 60 |
(1)填空:m=40,n=100,扇形统计图中扇形E组圆心角的度数为54°;
(2)若该市人口约有100万人,请你估计其中持“D组”观点的市民人数.
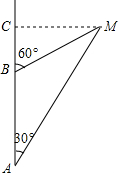 钓鱼岛自古就是中国的领土,中国有关部门己钓鱼岛及其附属岛屿开展常态化监视监测,一日,中国一艘海监船从A点沿正北方向以每小时24海里的速度巡航,在A点测得钓鱼岛中心M在点A的北偏东30°方向,问航行半小时后到达B点,测得钓鱼岛中心M在点B的北偏东60°方向,问再航行多少小时距离钓鱼岛中心最近?
钓鱼岛自古就是中国的领土,中国有关部门己钓鱼岛及其附属岛屿开展常态化监视监测,一日,中国一艘海监船从A点沿正北方向以每小时24海里的速度巡航,在A点测得钓鱼岛中心M在点A的北偏东30°方向,问航行半小时后到达B点,测得钓鱼岛中心M在点B的北偏东60°方向,问再航行多少小时距离钓鱼岛中心最近?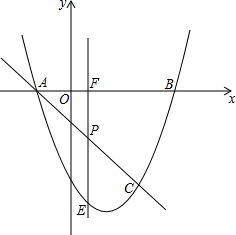 如图所示,抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),直线y=kx-1与抛物线y=x2-3x-4交于A,C两点.求A,B,C三点的坐标.
如图所示,抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),直线y=kx-1与抛物线y=x2-3x-4交于A,C两点.求A,B,C三点的坐标. 由一些大小相同、边长为1cm的小正方形组成的几何体的三视图如图所示,那么这个几何体表面积是22cm2,体积是5cm3.
由一些大小相同、边长为1cm的小正方形组成的几何体的三视图如图所示,那么这个几何体表面积是22cm2,体积是5cm3.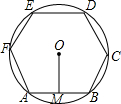 已知⊙O的内接正六边形ABCDEF的边心距OM为$\sqrt{3}$cm,则的⊙O半径为2cm.
已知⊙O的内接正六边形ABCDEF的边心距OM为$\sqrt{3}$cm,则的⊙O半径为2cm.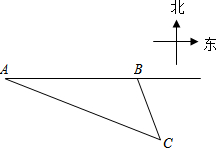 如图,我渔政船在东海海面上自西向东匀速巡航,在A地观测到某海岛C在东偏南21.3°方向上.若渔政船继续向东航行60海里到达B处,此时观测到海岛C在东偏南63.5°方向上.之后,渔政船再向东航多少海里,离海岛C的距离最近?
如图,我渔政船在东海海面上自西向东匀速巡航,在A地观测到某海岛C在东偏南21.3°方向上.若渔政船继续向东航行60海里到达B处,此时观测到海岛C在东偏南63.5°方向上.之后,渔政船再向东航多少海里,离海岛C的距离最近?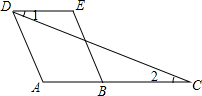 请将下列推理过程补充完整.
请将下列推理过程补充完整.