题目内容
16. 请将下列推理过程补充完整.
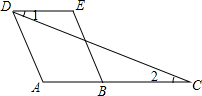
请将下列推理过程补充完整.已知:如图,点A、B、C在一条直线上,AD∥BE,∠1=∠2.
求证:∠A=∠E.
证明:∵AD∥BE
∵∠A=∠CBE(两直线平行,同位角相等)
又∵∠1=∠2
∴ED∥AC(内错角相等,两直线平行)
∴∠E=∠CBE(两直线平行,内错角相等)
∴∠A=∠E.
分析 由平行线的性质得出∠A=∠CBE,由内错角相等得出ED∥AC,由平行线的性质得出∠E=CBE,即可得出结论.
解答 证明:∵AD∥BE
∵∠A=∠CBE(两直线平行,同位角相等)
又∵∠1=∠2
∴ED∥AC(内错角相等,两直线平行)
∴∠E=CBE(两直线平行,内错角相等)
∴∠A=∠E.
故答案为:∠CBE;两直线平行,同位角相等;AC;内错角相等,两直线平行;∠CBE;两直线平行,内错角相等.
点评 本题考查了平行线的判定与性质;熟练掌握平行线的判定与性质是解决问题的关键,注意它们的区别.

练习册系列答案
相关题目
7.如果不等式组$\left\{\begin{array}{l}{x<5}\\{x<m}\end{array}\right.$的解集为x<5,那么m的取值范围是( )
| A. | m>5 | B. | m≥5 | C. | m<5 | D. | m≤5 |
4.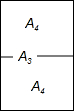 复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
 复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )| A. | 2:1 | B. | $\sqrt{2}$:1 | C. | $\sqrt{3}$:1 | D. | 3:1 |
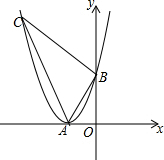 如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.
如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.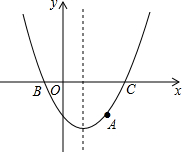 已知:二次函数的图象经过A(2,-3),对称轴x=1,抛物线与x轴两交点B、C的距离为4.
已知:二次函数的图象经过A(2,-3),对称轴x=1,抛物线与x轴两交点B、C的距离为4. 已知二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-1,-5.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1,x2,若x1=1.3,则x2的值为( )
已知二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-1,-5.2)及部分图象(如图),由图象可知关于x的一元二次方程ax2+bx+c=0的两个根分别是x1,x2,若x1=1.3,则x2的值为( )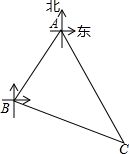 A,B,C三个城市的位置如图所示,城市B在城市A的西南方向(南偏西45°)100km处,城市C在城市A的南偏东30°方向,在城市B的南偏东75°方向.求城市A、C之间的距离.(结果取整数,参考数据:$\sqrt{6}$≈2.45)
A,B,C三个城市的位置如图所示,城市B在城市A的西南方向(南偏西45°)100km处,城市C在城市A的南偏东30°方向,在城市B的南偏东75°方向.求城市A、C之间的距离.(结果取整数,参考数据:$\sqrt{6}$≈2.45)