题目内容
15.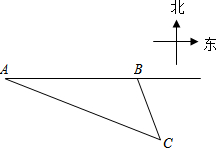 如图,我渔政船在东海海面上自西向东匀速巡航,在A地观测到某海岛C在东偏南21.3°方向上.若渔政船继续向东航行60海里到达B处,此时观测到海岛C在东偏南63.5°方向上.之后,渔政船再向东航多少海里,离海岛C的距离最近?
如图,我渔政船在东海海面上自西向东匀速巡航,在A地观测到某海岛C在东偏南21.3°方向上.若渔政船继续向东航行60海里到达B处,此时观测到海岛C在东偏南63.5°方向上.之后,渔政船再向东航多少海里,离海岛C的距离最近?(参考数据:sin21.3°≈$\frac{9}{25}$,tan21.3°$≈\frac{2}{5}$,sin63.5°$≈\frac{9}{10}$,tan63.5°≈2)
分析 首先过C作CD⊥AB,垂足为D,得到Rt△ACD与Rt△BCD,然后设BD=x海里,可得方程:xtan63.5°=(60+x)tan21.3°,继而求得答案.
解答 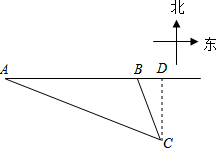 解:过C作CD⊥AB,垂足为D,得到Rt△ACD与Rt△BCD.
解:过C作CD⊥AB,垂足为D,得到Rt△ACD与Rt△BCD.
设BD=x海里,
在Rt△BCD中,tan∠CBD=$\frac{CD}{BD}$,
∴CD=xtan63.5°.
在Rt△ACD中,AD=AB+CD=(60+x)海里,tan∠A=$\frac{CD}{AD}$,
∴CD=(60+x)tan21.3°.
∴xtan63.5°=(60+x)tan21.3°,
即2x=$\frac{2}{5}$(60+x).
解得:x=15.
答:渔政船继续向东航行15海里,距离海岛C最近.
点评 此题考查了方向角问题.注意准确构造直角三角形是解此题的关键.

练习册系列答案
相关题目
7.如果不等式组$\left\{\begin{array}{l}{x<5}\\{x<m}\end{array}\right.$的解集为x<5,那么m的取值范围是( )
| A. | m>5 | B. | m≥5 | C. | m<5 | D. | m≤5 |
4.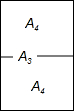 复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
 复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )| A. | 2:1 | B. | $\sqrt{2}$:1 | C. | $\sqrt{3}$:1 | D. | 3:1 |
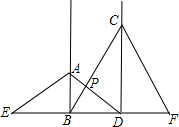 如图,工地上竖立着两根电线杆AB、CD,它们相距15m,分别自两杆上高出地面4m、6m的A、C处,向两侧地面上的E和D、B和F处用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD与BC的交点P离地面的高度PH是多少米?
如图,工地上竖立着两根电线杆AB、CD,它们相距15m,分别自两杆上高出地面4m、6m的A、C处,向两侧地面上的E和D、B和F处用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD与BC的交点P离地面的高度PH是多少米?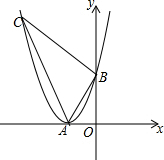 如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.
如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.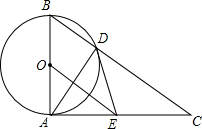 如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.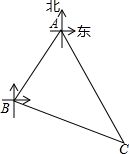 A,B,C三个城市的位置如图所示,城市B在城市A的西南方向(南偏西45°)100km处,城市C在城市A的南偏东30°方向,在城市B的南偏东75°方向.求城市A、C之间的距离.(结果取整数,参考数据:$\sqrt{6}$≈2.45)
A,B,C三个城市的位置如图所示,城市B在城市A的西南方向(南偏西45°)100km处,城市C在城市A的南偏东30°方向,在城市B的南偏东75°方向.求城市A、C之间的距离.(结果取整数,参考数据:$\sqrt{6}$≈2.45)