题目内容
1．
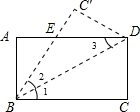如图，已知矩形ABCD沿着直线BD折叠，使点C落在C′处，BC′交AD于E，AD=4，AB=2，则DE的长=2.5．
分析 首先根据矩形的性质可得出AD∥BC，即∠1=∠3，然后根据折叠知∠1=∠2，C′D=CD、BC′=BC，可得到∠2=∠3，进而得出BE=DE，设DE=x，则EC′=4-x，利用勾股定理求出x的值，即可求出DE的长．
解答 解：∵四边形ABCD是矩形，
∴AD∥BC，即∠1=∠3，
∵由折叠的性质可知，∠1=∠2，C′D=CD=2，BC′=BC=4，
∴∠2=∠3，即DE=BE，
设DE=x，则EC′=4-x，
在Rt△DEC′中，DC'2+EC'2=DE2
∴22+（4-x）2=x2解得：x=2.5，
∴DE的长为2.5．
故答案为：2.5．
点评 本题主要考查的是翻折变换，解答本题的关键是掌握长方形的性质，勾股定理的利用以及折叠的知识，此题比较简单．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
11．
某单位在植树节派出50名员工植树造林，统计每个人植树的棵树之后，绘制成如图所示的频数分布直方图（图中分组含最低值，不含最高值），则植树7棵以上的人数占总人数的（ ）
某单位在植树节派出50名员工植树造林，统计每个人植树的棵树之后，绘制成如图所示的频数分布直方图（图中分组含最低值，不含最高值），则植树7棵以上的人数占总人数的（ ）| A． | 40% | B． | 70% | C． | 76% | D． | 96% |
12．
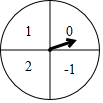如图是一次数学活动课制作的一个转盘，盘面被等分成四个扇形区域，并分别标有数字-1，0，1，2．若转动转盘两次，每次转盘停止后记录指针所指区域的数字（当指针恰好指在分界线上时，不记，重转），则记录的两个数字都是正数的概率为（ ）
如图是一次数学活动课制作的一个转盘，盘面被等分成四个扇形区域，并分别标有数字-1，0，1，2．若转动转盘两次，每次转盘停止后记录指针所指区域的数字（当指针恰好指在分界线上时，不记，重转），则记录的两个数字都是正数的概率为（ ）| A． | $\frac{1}{8}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{2}$ |
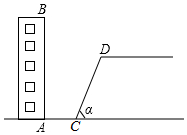如图，某校教学楼AB后方有一斜坡，已知斜坡CD的长为12米，坡角α为60°，根据有关部门的规定，∠α≤39°时，才能避免滑坡危险，学校为了消除安全隐患，决定对斜坡CD进行改造，在保持坡脚C不动的情况下，学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全？（结果取整数）
6．下列实数中，是无理数的为（ ）
| A． | $\frac{1}{3}$ | B． | $\sqrt{7}$ | C． | $\sqrt{4}$ | D． | 3.14 |
已知抛物线y=x2-2x-a．