题目内容
17.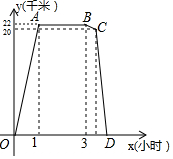 某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.
某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.(1)活动中心与小宇家相距22千米,小宇在活动中心活动时间为2小时,他从活动中心返家时,步行用了0.4小时;
(2)求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);
(3)根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.
分析 (1)根据点A、B坐标结合时间=路程÷速度,即可得出结论;
(2)根据离家距离=22-速度×时间,即可得出y与x之间的函数关系式;
(3)由小宇步行的时间等于爸爸开车接到小宇的时间结合往返时间相同,即可求出小宇从活动中心返家所用时间,将其与1比较后即可得出结论.
解答 解:(1)∵点A的坐标为(1,22),点B的坐标为(3,22),
∴活动中心与小宇家相距22千米,小宇在活动中心活动时间为3-1=2小时.
(22-20)÷5=0.4(小时).
故答案为:22;2;0.4.
(2)根据题意得:y=22-5(x-3)=-5x+37.
(3)小宇从活动中心返家所用时间为:0.4+0.4=0.8(小时),
∵0.8<1,
∴小宇12:00前能到家.
点评 本题考查了一次函数的应用,解题的关键是:(1)根据数量关系列式计算;(2)根据离家距离=22-速度×时间,找出y与x之间的函数关系式;(3)由爸爸开车的速度不变,求出小宇从活动中心返家所用时间.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.小林在某商店购买商品A、B共三次,在三次购买中,只有一次购买的商品A、B同时打折,其余两次均按原标价购买,三次购买商品A、B的数量与费用如表:
(1)小林第三次购物时,商店有打折(直接写出即可)
(2)求出商品A,B的原标价.
(3)若商品A、B打折后的价格分别为原价的x%,y%(x、y均为10的整数倍),则按此优惠标准,小林一次性购买这三次商品的总费用比全部按原标价购买优惠1524元.
| 购买商品A的数量 | 购买商品B的数量 | 购买总费用(元) | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 | 1128 |
(2)求出商品A,B的原标价.
(3)若商品A、B打折后的价格分别为原价的x%,y%(x、y均为10的整数倍),则按此优惠标准,小林一次性购买这三次商品的总费用比全部按原标价购买优惠1524元.
12.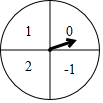 如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )
如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )
 如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )
如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
2. 如图所示,所给的三视图表示的几何体是( )
如图所示,所给的三视图表示的几何体是( )
 如图所示,所给的三视图表示的几何体是( )
如图所示,所给的三视图表示的几何体是( )| A. | 圆锥 | B. | 正三棱锥 | C. | 正四棱锥 | D. | 正三棱柱 |
6.下列实数中,是无理数的为( )
| A. | $\frac{1}{3}$ | B. | $\sqrt{7}$ | C. | $\sqrt{4}$ | D. | 3.14 |
2.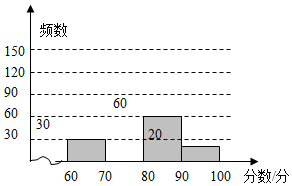 为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
请根据以上图表提供的信息,解答下列问题:
(1)这次共调查了200名学生;表中的数m=90,n=0.3;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是54°;
(4)如果比赛成绩在80分以上(含80分)可获得奖励,那么获奖概率是多少?
 为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | m | 0.45 |
| 80≤x<90 | 60 | n |
| 90≤x≤100 | 20 | 0.1 |
(1)这次共调查了200名学生;表中的数m=90,n=0.3;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是54°;
(4)如果比赛成绩在80分以上(含80分)可获得奖励,那么获奖概率是多少?