题目内容
10．
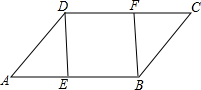如图所示，已知AB=CD，AD=BC，DE=BF，且E，F分别是AB，CD的中点．（1）求证：∠A=∠C．
（2）求证：∠EDF=∠FBE．
分析 （1）首先求出AE=CF，结合题干条件利用SSS证明△DAE≌△BCF，结论即可得出；
（2）利用平行四边形的性质即可得到结论．
解答 解：（1）∵AB=CD，E，F分别是AB，CD的中点，
∴AE=CF，DF=BE，
在△DAE和△BCF中，
∵$\left\{\begin{array}{l}{AD=BC}\\{AE=CF}\\{DE=BF}\end{array}\right.$，
∴△DAE≌△BCF，
∴∠A=∠C；
（2）∵AD=BC，AB=CD，
∴四边形ABCD是平行四边形，
∴AB∥CD，
∵DF=BE，
∴四边形DEBF是平行四边形，
∴∠EDF=∠FBE．
点评 本题主要考查了全等三角形的判定与性质以及平行四边形的知识，解题的关键是熟练掌握SSS证明三角形全等以及平行四边形的性质，此题难度不大．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
1．为确保信息安全，信息需加密传输，发送方由明文→密文（加密）；接收方由密文→明文（解密）．已知加密规则为：明文a，b，c对应密文a+2b，2b+c，3c．例如：明文1，2，3对应的密文5，7，9．当接收方收到密文14，9，15时，则解密得到的明文为（ ）
| A． | 10，5，2 | B． | 10，2，5 | C． | 2，5，10 | D． | 5，10，2 |
18．
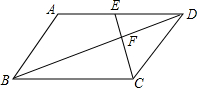如图，在平行四边形ABCD中，E为AD的中点，△DEF的周长为1，则△BCF的周长为（ ）
如图，在平行四边形ABCD中，E为AD的中点，△DEF的周长为1，则△BCF的周长为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
已知AB⊥BC，AD⊥DC，且BC=DC，求证：∠ABD=∠ADB．