题目内容
14.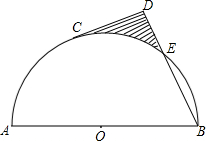 如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )
如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )| A. | 8$\sqrt{3}$-4π | B. | 8$\sqrt{3}$-$\frac{8}{3}$π | C. | 4π-6$\sqrt{3}$ | D. | 6$\sqrt{3}$-$\frac{8}{3}$π |
分析 连接OC,OE,作OF⊥BE于F,根据题意求得∠AOC=60°,∠BOC=120°,根据切线性质进一步得出OC∥BD,得出∠B=∠AOC=60°,从而求得△EOB是等边三角形,解直角三角形求得EF和OF,然后根据S阴影=S矩形-S扇形OCE-S△EOF即可求得.
解答 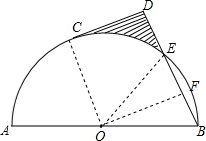 解:连接OC,OE,作OF⊥BE于F,
解:连接OC,OE,作OF⊥BE于F,
∵DC是半圆0的切线,
∴OC⊥CD,
∵BD⊥CD,
∴OC∥BD,
∵$\widehat{BC}$=2$\widehat{AC}$,
∴∠AOC=60°,∠BOC=120°,
∴∠B=∠AOC=60°,
∵OB=OE,
∴△EOB是等边三角形,
∴∠EOB=60°,
∴∠COE=60°,
∵OC⊥CD,BD⊥CD,OF⊥BD,
∴四边形OCDF是矩形,
∴DF=OC=4,
在RT△BOF中,∠B=60°,
∴BF=$\frac{1}{2}$OB=2,OF=$\frac{\sqrt{3}}{2}$OB=2$\sqrt{3}$,
∴EF=BF=2,
∴S阴影=S矩形-S扇形OCE-S△EOF
=4×2$\sqrt{3}$-$\frac{60π×{4}^{2}}{360}$-$\frac{1}{2}$×2×2$\sqrt{3}$
=6$\sqrt{3}$-$\frac{8}{3}$π.
故选D.
点评 本题考查了切线的性质,平行线的判定,等边三角形的判定和性质,解直角三角形以及扇形的面积等,作出辅助线构建矩形和等边三角形是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
6.下列同类二次根式合并过程正确的是( )
| A. | 2$\sqrt{3}$-$\sqrt{3}$=2 | B. | a$\sqrt{c}$+b$\sqrt{c}$=a+b$\sqrt{c}$ | C. | 5$\sqrt{a}$+$\frac{1}{2}$$\sqrt{a}$=5+$\frac{1}{2}$$\sqrt{a}$ | D. | $\frac{1}{3}$$\sqrt{3a}$-$\frac{1}{4}$$\sqrt{3a}$=$\frac{1}{12}$$\sqrt{3a}$ |
9.化简$\frac{x-y}{\sqrt{x}+\sqrt{y}}$,甲、乙两位同学的解法如下:
甲:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(x-y)(\sqrt{x}-\sqrt{y})}{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}$=$\sqrt{x}$-$\sqrt{y}$;
乙:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$-$\sqrt{y}$.
对于甲、乙两位同学的解法,正确的判断是( )
甲:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(x-y)(\sqrt{x}-\sqrt{y})}{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}$=$\sqrt{x}$-$\sqrt{y}$;
乙:$\frac{x-y}{\sqrt{x}+\sqrt{y}}$=$\frac{(\sqrt{x}+\sqrt{y})(\sqrt{x}-\sqrt{y})}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$-$\sqrt{y}$.
对于甲、乙两位同学的解法,正确的判断是( )
| A. | 甲、乙都正确 | B. | 甲正确,乙不正确 | C. | 甲、乙都不正确 | D. | 乙正确,甲不正确 |
19. 由一些大小相同的小正方体组成的几何体主视图和俯视图如图所示,小正方体的块数可能有( )种.
由一些大小相同的小正方体组成的几何体主视图和俯视图如图所示,小正方体的块数可能有( )种.
 由一些大小相同的小正方体组成的几何体主视图和俯视图如图所示,小正方体的块数可能有( )种.
由一些大小相同的小正方体组成的几何体主视图和俯视图如图所示,小正方体的块数可能有( )种.| A. | 5种 | B. | 6种 | C. | 7种 | D. | 8种 |
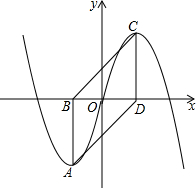 如图,在平面直角坐标系中,过抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点C作CD⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为4.
如图,在平面直角坐标系中,过抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点C作CD⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为4.