题目内容
5.分式方程$\frac{{{x^2}-1}}{x-1}=0$的解是x=-1.分析 根据分式方程,可以先去分母变为整式方程进行解答,解出整式方程的根注意要进行检验.
解答 解:$\frac{{{x^2}-1}}{x-1}=0$
方程两边同乘以x-1得,
x2-1=0
则(x+1)(x-1)=0
∴x+1=0或x-1=0
得,x=-1或x=1.
检验:x=-1时,x-1≠0;x=1时,x-1=0,故x=1舍去.
故分式方程的根为:x=-1.
故答案为:x=-1.
点评 本题考查解答分式方程,解题的关键是解出方程的根要检验.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
13.方程(x-2)(x-3)=6的两根分别为( )
| A. | 2或3 | B. | 5或0 | C. | 5或1 | D. | 4或6 |
10. 如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,OA=2,则图中阴影部分的面积为( )
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,OA=2,则图中阴影部分的面积为( )
 如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,OA=2,则图中阴影部分的面积为( )
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,OA=2,则图中阴影部分的面积为( )| A. | $\frac{4π}{3}$-$\sqrt{3}$ | B. | $\frac{4π}{3}$-2$\sqrt{3}$ | C. | π-$\sqrt{3}$ | D. | $\frac{π}{3}$-$\frac{\sqrt{3}}{4}$ |
14.化简(a+1)+a(a+1)+a(a+1)2+…+a(a+1)2015等于( )
| A. | (a+1)2014 | B. | (a+1)2015 | C. | (a+1)2016 | D. | (a+1)2017 |
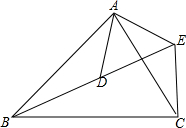 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,请猜想∠BAD与∠CAE的关系,并说明理由.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,请猜想∠BAD与∠CAE的关系,并说明理由.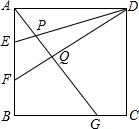 如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P、Q,S四边形GCDQ:S四边形BGQF==17:9.
如图,正方形ABCD中,AE=EF=FB,BG=2CG,DE,DF分别交AG于P、Q,S四边形GCDQ:S四边形BGQF==17:9.