题目内容
12.阅读材料:如果x1、x2是一元二次方程ax2+bx+c=0(a≠0)的两根,那么,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.这就是著名的韦达定理.现在我们利用韦达定理解决问题:
已知m与n是方程2x2-6x-5=0的两根
(1)填空:m+n=3,m•n=-$\frac{5}{2}$;
(2)计算$\frac{2}{m}$+$\frac{2}{n}$的值;
(3)计算(m-n)2的值.
分析 (1)根据韦达定理求解;
(2)先把原式通分,然后利用整体代入的方法计算;
(3)先利用完全平方公式变形得到原式=(m+n)2-4 mn,然后利用整体代入的方法计算.
解答 解:(1)m+n=-$\frac{-6}{2}$=3,mn=-$\frac{5}{2}$;
(2)原式=$\frac{2(m+n)}{mn}$=$\frac{2×3}{-\frac{5}{2}}$=-$\frac{12}{5}$;
(3)原式=(m+n)2-4 mn=32-4×(-$\frac{5}{2}$)=19.
故答案为3,-$\frac{5}{2}$.
点评 本题考查了根与系数的关系:如果x1、x2是一元二次方程ax2+bx+c=0(a≠0)的两根,那么,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
3.下列命题中,
①长为5cm的线段AB沿某一方向平移10cm后,平移后线段AB的长为10cm
②三角形的高在三角形内部
③六边形的内角和是外角和的两倍
④平行于同一直线的两条直线平行
⑤两个角的两边分别平行,则这两个角相等.
真命题个数有( )
①长为5cm的线段AB沿某一方向平移10cm后,平移后线段AB的长为10cm
②三角形的高在三角形内部
③六边形的内角和是外角和的两倍
④平行于同一直线的两条直线平行
⑤两个角的两边分别平行,则这两个角相等.
真命题个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.下列说法正确的是( )
| A. | 0.03780有五个有效数字 | |
| B. | 方差越大,数据波动也越大 | |
| C. | 58°的余角是42° | |
| D. | 投掷一枚硬币10次,“正面向上”一定出现5次 |
4.下列各数-3,$\frac{π}{2}$,3.121121112…,0,$\frac{22}{7}$中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.下列运算正确的是( )
| A. | a3-a2=a | B. | a2•a3=a6 | C. | (-3a)3=-9a3 | D. | (-a3)2=a6 |
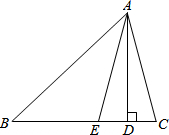 如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=45°,∠C=75°,求∠DAE的度数.
如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=45°,∠C=75°,求∠DAE的度数. 如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,求△ADE的周长.
如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,求△ADE的周长.