题目内容
2.计算:(1)$\sqrt{32}$-$\sqrt{8}$+2$\sqrt{\frac{1}{2}}$
(2)$\frac{2}{3}\sqrt{9x}$-(6$\sqrt{\frac{x}{4}}-2x\sqrt{\frac{1}{x}}$)
分析 (1)先把各根式化为最减二次根式,再合并同类项即可;
(2)先去括号,把各根式化为最减二次根式,再合并同类项即可.
解答 解:(1)原式=4$\sqrt{2}$-2$\sqrt{2}$+$\sqrt{2}$
=3$\sqrt{2}$;
(2)原式=2$\sqrt{x}$-3$\sqrt{x}$+2$\sqrt{x}$
=$\sqrt{x}$.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,△ABC与△DBC有共同底边BC,且∠BAC=∠BDC,AC交BD于点E,连接AD.求证:∠1=∠2.
如图,△ABC与△DBC有共同底边BC,且∠BAC=∠BDC,AC交BD于点E,连接AD.求证:∠1=∠2. 如图,在△ABC中,CD平分∠ACB,DE∥AC,∠B=50°,∠EDC=30°.求∠ADC的度数.
如图,在△ABC中,CD平分∠ACB,DE∥AC,∠B=50°,∠EDC=30°.求∠ADC的度数. 如图,已知线段AB=6.
如图,已知线段AB=6. 如图,在正方形ABCD中,点E是AD的中点,连接BE、CE,点F是CE的中点,连接DF、BF,点M是BF上一点且$\frac{BM}{MF}$=$\frac{1}{2}$,过点M作MN⊥BC于点N,连接FN,下列结论中:①BE=CE;②∠BEF=∠DFE;③MN=$\frac{1}{6}$AB;④$\frac{{S}_{△FMN}}{{S}_{四边形EBNF}}$=$\frac{1}{6}$,其中正确结论的序号分别是①②③.
如图,在正方形ABCD中,点E是AD的中点,连接BE、CE,点F是CE的中点,连接DF、BF,点M是BF上一点且$\frac{BM}{MF}$=$\frac{1}{2}$,过点M作MN⊥BC于点N,连接FN,下列结论中:①BE=CE;②∠BEF=∠DFE;③MN=$\frac{1}{6}$AB;④$\frac{{S}_{△FMN}}{{S}_{四边形EBNF}}$=$\frac{1}{6}$,其中正确结论的序号分别是①②③.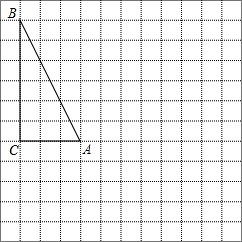 在如图所示的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=6.
在如图所示的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=6.