题目内容
7.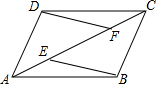 如图,E、F是?ABCD对角线AC上两点,AE=CF.
如图,E、F是?ABCD对角线AC上两点,AE=CF.(1)求证:△ABE≌△CDF;
(2)连结DE,BF,求证:四边形DEBF是平行四边形.
分析 (1)由平行四边形的性质得出∠BAE=∠DCF,由SAS证明△ABE≌△CDF即可;
(2)由全等三角形的性质得出BE=DF,同理:DE=BF,即可得出结论.
解答 (1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,$\left\{\begin{array}{l}{AE=CF}&{\;}\\{∠BAE=∠DCF}&{\;}\\{AB=CD}&{\;}\end{array}\right.$,
∴△ABE≌△CDF(SAS);
(2)证明:连接DE、BF,如图所示:
由(1)得:△ABE≌△CDF,
∴BE=DF,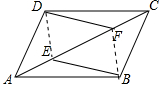 同理:DE=BF,
同理:DE=BF,
∴四边形DEBF是平行四边形.
点评 本题考查了平行四边形的性质与判定、全等三角形的判定与性质;熟练掌握平行四边形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
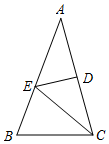 如图,△ABC中,∠A=36°,AC的垂直平分线交AB于E,D为垂足,AB=AC,连结EC.
如图,△ABC中,∠A=36°,AC的垂直平分线交AB于E,D为垂足,AB=AC,连结EC.
 如图,四边形ABCD中,AD∥BC,∠A=∠C,试判别四边形ABCD的形状,并说明理由.
如图,四边形ABCD中,AD∥BC,∠A=∠C,试判别四边形ABCD的形状,并说明理由.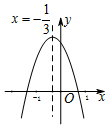 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息: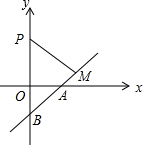 如图,在平面直角坐标系中,点P的坐标为(0,2$\sqrt{3}$),直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x轴,y轴分别交于A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{9}{5}$.
如图,在平面直角坐标系中,点P的坐标为(0,2$\sqrt{3}$),直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x轴,y轴分别交于A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{9}{5}$.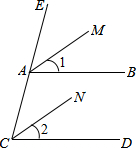 如图,已知AM∥CN,且∠1=∠2,那么AB∥CD吗?为什么?
如图,已知AM∥CN,且∠1=∠2,那么AB∥CD吗?为什么?