题目内容
17.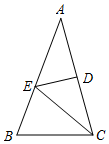 如图,△ABC中,∠A=36°,AC的垂直平分线交AB于E,D为垂足,AB=AC,连结EC.
如图,△ABC中,∠A=36°,AC的垂直平分线交AB于E,D为垂足,AB=AC,连结EC.(1)求∠ECD的度数;
(2)猜想△BCE的形状并证明.
分析 (1)根据线段垂直平分线得出AE=CE,推出∠ECD=∠A即可;
(2)根据等腰三角形的性质得到∠B=∠ACB=72°,推出∠B=∠BEC,于是得到结论.
解答 解:(1)∵DE垂直平分AC,
∴CE=AE,
∴∠ECD=∠A=36°;
(2)△BCE是等腰三角形,
证明:∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∵∠ECD=36°,
∴∠BCE=36°,
∴∠BEC=72°,
∴∠B=∠BEC,
∴△BCE是等腰三角形.
点评 本题考查了等腰三角形的判定和性质,三角形的内角和,熟练掌握等腰三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
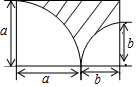 在如图所示的长方形中,请用含字母a,b的代数式表示阴影面积,并按字母a降幂排列得(1-$\frac{1}{4}$π)a2+ab-$\frac{1}{4}$πb2.
在如图所示的长方形中,请用含字母a,b的代数式表示阴影面积,并按字母a降幂排列得(1-$\frac{1}{4}$π)a2+ab-$\frac{1}{4}$πb2.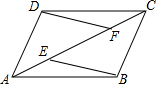 如图,E、F是?ABCD对角线AC上两点,AE=CF.
如图,E、F是?ABCD对角线AC上两点,AE=CF.