题目内容
12.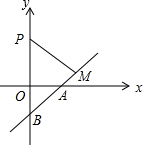 如图,在平面直角坐标系中,点P的坐标为(0,2$\sqrt{3}$),直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x轴,y轴分别交于A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{9}{5}$.
如图,在平面直角坐标系中,点P的坐标为(0,2$\sqrt{3}$),直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x轴,y轴分别交于A,B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{9}{5}$.
分析 当PM⊥直线AB时,此时PM有最小值,利用直线y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$求出点A与B的坐标,从而可知OA,OB的长度,然后证明△AOB∽△BMP,利用相似三角形的性质即可求出PM的值.
解答 解:当PM⊥直线AB时,此时PM有最小值,
令x=0代入y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$,
∴y=-$\sqrt{3}$,
∴OB=$\sqrt{3}$,
令y=0代入y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$求,
∴x=3,
∴OA=3,
∴在Rt△AOB中,
由勾股定理可知:AB=2$\sqrt{3}$,
∵P(0,2$\sqrt{3}$),
∴BP=2$\sqrt{3}$+$\sqrt{3}$=3$\sqrt{3}$
∵∠OBA=∠MBP,∠AOB=∠PMB=90°,
∴△AOB∽△BMP
∴$\frac{PM}{BP}$=$\frac{OA}{AB}$,
∴PM=$\frac{9}{2}$
故答案为:$\frac{9}{2}$
点评 本题考查垂线段最短,解题的关键是求出OA、OB、AB的长度,从而可求出答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.多项式$\frac{1}{2}$x|m|y-(m-3)xy+7是关于x、y的四次三项式,则m的值是( )
| A. | 3或-3 | B. | -3 | C. | 4或-4 | D. | 3 |
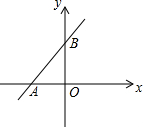 如图,直线y=5x+10与x轴、y轴交于点A,B,则△AOB的面积为10.
如图,直线y=5x+10与x轴、y轴交于点A,B,则△AOB的面积为10.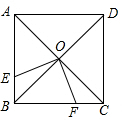 如图,正方形ABCD的对角线AC、BD相交于点O,点E、F分别在边AB、BC上,且∠EOF=90°,则S四边形OEBF:S正方形ABCD=$\frac{1}{4}$.
如图,正方形ABCD的对角线AC、BD相交于点O,点E、F分别在边AB、BC上,且∠EOF=90°,则S四边形OEBF:S正方形ABCD=$\frac{1}{4}$.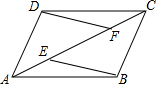 如图,E、F是?ABCD对角线AC上两点,AE=CF.
如图,E、F是?ABCD对角线AC上两点,AE=CF.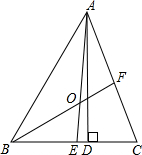 如图,在△ABC中,AD是高,AE,BF是角平分线,AE和BF交于点O,∠BAC=58°,∠BOA=125°,求∠C和∠DAE的度数.
如图,在△ABC中,AD是高,AE,BF是角平分线,AE和BF交于点O,∠BAC=58°,∠BOA=125°,求∠C和∠DAE的度数.