题目内容
16.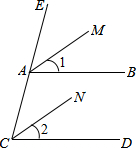 如图,已知AM∥CN,且∠1=∠2,那么AB∥CD吗?为什么?
如图,已知AM∥CN,且∠1=∠2,那么AB∥CD吗?为什么?解:因为AM∥CN ( 已知 )
所以∠EAM=∠ECN两直线平行,同位角相等
又因为∠1=∠2已知
所以∠EAM+∠1=∠ECN+∠2等式性质
即∠BAE=∠DCE
所以AB∥CD.
分析 利用两直线平行,同位角相等即可得到一对同位角相等,利用等式的性质得到另一对同位角相等,最后利用同位角相等,两直线平行即可得证.
解答  解:因为AM∥CN (已知),
解:因为AM∥CN (已知),
所以∠EAM=∠ECN(两直线平行,同位角相等),
又因为∠1=∠2(已知),
所以∠EAM+∠1=∠ECN+∠2(等式性质),
即∠BAE=∠DCE,
所以AB∥CD.
故答案为:两直线平行,同位角相等;已知;等式性质;BAE,DCE;AB∥CD.
点评 此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
相关题目
11.x=2是方程ax-6=0的解,则a的取值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
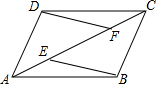 如图,E、F是?ABCD对角线AC上两点,AE=CF.
如图,E、F是?ABCD对角线AC上两点,AE=CF.