题目内容
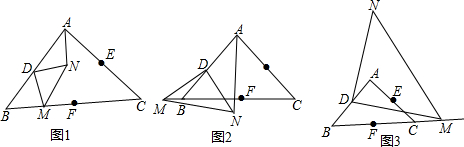
4.如图,已知等腰直角三角形ABC中,D、E、F分别为边AB、AC、BC的中点,点M为斜边BC所在直线上一动点,且三角形DMN为等腰直角三角形(DM=DN,D、M、N呈逆时针).(1)如图1点M在边BC上,判断MF和AN的数量和位置关系,请直接写出你的结论.
(2)如图2点M在B点左侧时;如图3,点M在C点右侧.其他条件不变,(1)中结论是否仍然成立,并选择图2或图3的一种情况来说明理由.
(3)在图2中若∠DMB=α,连接EN,请猜测MF与EN的数量关系,即MF=(sinα+cosα) EN.(用含α的三角函数的式子表示)
分析 (1)可通过全等三角形来证明AN与MF相等,如果连接DF,那么DF就是三角形ABC的中位线,可得出三角形BDF是等腰直角三角形,那么∠DFM=∠C=45°,DB=DF,而∠MDF=∠ADN,因此△FDM≌△AFN,由此可得出AN=MF,∠DAN=∠DFM=45°,由等腰三角形三线合一的性质得出AN⊥MF;
(2)证法同(1);
(3)证明△DAN≌△EAN,得出EN=DN,进一步得出DM=EN,作DH⊥BC于H,由∠DFM=45°,证得△DHF是等腰直角三角形,得出FH=DH,然后解直角三角形得出MH=DM•sinα,DH=DM•cosα,从而得出MF=MH+FH=DM(sinα+cosα)=(sinα+cosα)EN.
解答 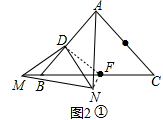 解:(1)判断:AN=MF且AN⊥MF,
解:(1)判断:AN=MF且AN⊥MF,
(2)成立.
连接DF,NF,如图2①,
∵△ABC是等腰直角三角形,
∴AB=AC,∠BAC=90°.
又∵D,E,F是三边的中点,
∴DF∥AC,DF=$\frac{1}{2}$AC=$\frac{1}{2}$AB=AD,
∴∠BDF=90°,∠MFD=∠C=45°,
∴∠MDN=∠BDF,
∴∠FDM=∠ADN,
在△DMF和△DNA中,
$\left\{\begin{array}{l}{DF=AD}\\{∠FDM=∠ADN}\\{DM=DN}\end{array}\right.$
∴△DMF≌△DNA(SAS),
∴FM=AN,∠DAN=∠MFD=45°.
∴AN是∠BAC的平分线,
∴AN⊥BC,
即AN⊥MF;
(3)由(2)可知:∠DAN=∠EAN,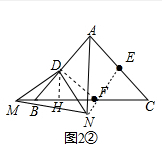 如图2②,
如图2②,
∵D、E分别为边AB、ACC的中点,AB=AC,
∴AD=AE,
在△DAN和△EAN中,
$\left\{\begin{array}{l}{AD=AE}\\{∠DAN=∠EAN}\\{AN=AN}\end{array}\right.$
∴△DAN≌△EAN(SAS),
∴EN=DN,
∵DM=DN,
∴DM=EN,
作DH⊥BC于H,
∵∠DFM=45°,
∴△DHF是等腰直角三角形,
∴FH=DH,
∵MH=DM•sinα,DH=DM•cosα,
∴FH=DH=DM•cosα,
∴MF=MH+FH=DM(sinα+cosα)=(sinα+cosα)EN,
即MF=(sinα+cosα)EN;
故答案为(sinα+cosα).
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的判定和性质,解直角三角形等,作出辅助线构建全等三角形是解题的关键.

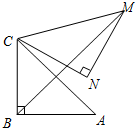 如图,Rt△ABC中,∠ABC=90°,AB=BC=2,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,那么BM的长是$\sqrt{6}+\sqrt{2}$.
如图,Rt△ABC中,∠ABC=90°,AB=BC=2,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,那么BM的长是$\sqrt{6}+\sqrt{2}$. 如图,在△ABC中,∠CAB=90°,AB=6,AC=4,CD是△ABC的中线,将△ABC沿直线CD翻折,点B′是点B的对应点,点E是线段CD上的点,如果∠CAE=∠BAB′,那么CE的长是$\frac{16}{5}$.
如图,在△ABC中,∠CAB=90°,AB=6,AC=4,CD是△ABC的中线,将△ABC沿直线CD翻折,点B′是点B的对应点,点E是线段CD上的点,如果∠CAE=∠BAB′,那么CE的长是$\frac{16}{5}$.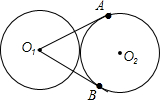 如图,两个等圆⊙O1和⊙O2外切,过点O1作⊙O2的两条切线OA、OB,A、B为切点,则∠AO1B=60°.
如图,两个等圆⊙O1和⊙O2外切,过点O1作⊙O2的两条切线OA、OB,A、B为切点,则∠AO1B=60°.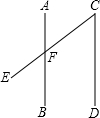 如图,AB∥CD,∠AFE=125°,则∠C的度数为55°.
如图,AB∥CD,∠AFE=125°,则∠C的度数为55°.


