题目内容
1.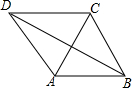 已知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b.求cos∠DBA的值.
已知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b.求cos∠DBA的值.
分析 欲求∠DBA的余弦值,需将已知条件构建到一个直角三角形中求解;已知四边形ABCD中,AB=AC=AD;若以A为圆心,AB为半径作圆,则此圆必过C、D;延长BA交⊙A于E,则BE为⊙A的直径,连接DE,在Rt△BDE中,已知了BE=2a,需求出BD的长;根据DC∥AB,易证得DE=BC=b,则根据勾股定理即可求得BD的长,由此得解.
解答 解:如图,以A为圆心,以a为半径作圆.延长BA交⊙A于E点,连接ED,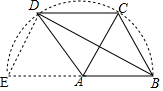
∵AB∥CD,
∴∠CAB=∠DCA,∠DAE=∠CDA;
∵AC=AD,∴∠DCA=∠CDA,
∴∠DAE=∠CAB,
在△ABC和△DAE中,
∵$\left\{\begin{array}{l}{AD=AC}\\{∠DAE=∠CAB}\\{AE=AB}\end{array}\right.$,
∴△CAB≌△DAE(SAS),
∴ED=BC=b,
∵BE是直径,
∴∠EDB=90°
在Rt△EDB中,ED=b,BE=2a,
由勾股定理得ED2+BD2=BE2
∴BD=$\sqrt{B{E}^{2}-E{D}^{2}}$=$\sqrt{(2a)^{2}-{b}^{2}}$=$\sqrt{4{a}^{2}-{b}^{2}}$,
∴cos∠DBA=$\frac{BD}{BE}$=$\frac{\sqrt{4{a}^{2}-{b}^{2}}}{2a}$.
点评 此题主要考查了圆周角定理、勾股定理以及全等三角形的判定;能够通过辅助线构建出⊙A是解答本题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
9.已知x,y是实数,$\sqrt{3x+4}$+y2+6y+9=0,若axy-3x=y,则实数a的值是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{7}{4}$ | D. | -$\frac{7}{4}$ |
16. 如图,4个小圆的面积相等,大圆的半径等于小圆的直径,则图中阴影部分的面积S1与大圆的面积S2的大小关系为( )
如图,4个小圆的面积相等,大圆的半径等于小圆的直径,则图中阴影部分的面积S1与大圆的面积S2的大小关系为( )
 如图,4个小圆的面积相等,大圆的半径等于小圆的直径,则图中阴影部分的面积S1与大圆的面积S2的大小关系为( )
如图,4个小圆的面积相等,大圆的半径等于小圆的直径,则图中阴影部分的面积S1与大圆的面积S2的大小关系为( )| A. | S1=S2 | B. | S1=$\frac{1}{2}$S2 | C. | S1=$\frac{1}{3}$S2 | D. | S1=$\frac{1}{4}$S2 |
 如图是一个破残的车轮,请用尺规作图法补全车轮并标出圆心O.
如图是一个破残的车轮,请用尺规作图法补全车轮并标出圆心O. 如图,Rt△ABC中,∠C=90°,AC=12,BC=9,点P从点A出发,以每秒5个单位的速度向点B匀速运动,同时点Q从点C出发.向点A匀速运动,结果两点同时到目的地.设运动的时间为1.
如图,Rt△ABC中,∠C=90°,AC=12,BC=9,点P从点A出发,以每秒5个单位的速度向点B匀速运动,同时点Q从点C出发.向点A匀速运动,结果两点同时到目的地.设运动的时间为1.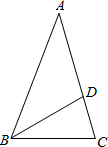 如图,已知△ABC,AB=AC=2,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是$\sqrt{5}$-1.
如图,已知△ABC,AB=AC=2,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是$\sqrt{5}$-1.