Question

13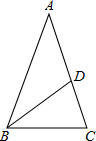．如图，在△ABC中，AB=AC，∠A=36°，BD是∠ABC的角平分线．
（1）求证：△ABC∽△BDC；
（2）求证：点D是线段AC的黄金分割点．

Answer 1

分析 （1）根据等腰三角形的性质、角平分线的定义求出∠A=∠CDB，证明△ABC∽△BDC；
（2）根据相似三角形的性质得到BC²=AC•CD，证明BC=AD，根据黄金分割的概念解答即可．

解答 （1）证明：∵AB=AC，∠A=36°，
∴∠ABC=∠ACB=72°，
∵BD是∠ABC的角平分线，
∴∠ABD=∠DBC=36°，
∴∠A=∠CDB，又∠C=∠C，
∴△ABC∽△BDC；
（2）解：∵△ABC∽△BDC，
∴$\frac{CD}{BC}$=$\frac{BC}{AC}$，
∴BC²=AC•CD，
∵∠A=∠ABD，
∴DA=DB，
∵∠C=∠BDC，
∴BC=DB，
∴BC=AD，
∴AD²=AC•CD．

点评 本题考查的是等腰三角形的性质、黄金分割的概念，掌握相似三角形的判定定理和性质定理、黄金分割的概念是解题的关键．