题目内容
14.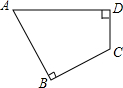 如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,BC=2,CD=1,求AD的长.
如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,BC=2,CD=1,求AD的长.
分析 延长AD,DC交于点E,可得直角三角形ABE,易得CE长,在Rt△CBE中,利用30°的三角函数可得EC,DE的长,进而利用勾股定理可得AD长.
解答  解:分别延长AD、DC交于点E,
解:分别延长AD、DC交于点E,
在Rt△ABE中,∵∠A=60°,
∴∠E=30°,
在Rt△CBE中,∵∠E=30°,BC=2,
∴EC=4,
∴DE=4+1=5,
在Rt△ABE中,∠E=30°,
AE=2AD,
AE2=AD2+DE2,
4AD2=AD2+52,
解得:AD=$\frac{{5\sqrt{3}}}{3}$.
点评 考查了勾股定理,解直角三角形的知识;作辅助线构造出特殊的直角三角形是解决本题的难点.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
2.要使a5<a3<a<a2<a4成立,则a的取值范围是( )
| A. | 0<a<1 | B. | a>1 | C. | -1<a<0 | D. | a<-1 |
9.已知x,y是实数,$\sqrt{3x+4}$+y2+6y+9=0,若axy-3x=y,则实数a的值是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{7}{4}$ | D. | -$\frac{7}{4}$ |
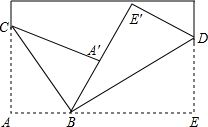 如图所示,将一张长方形纸片斜折过去,使顶点A落在 A′处,BC为折痕,然后再把BE折过去,使之与BA重合,折痕为BD,若∠ABC=58°,则求∠E′BD的度数是32°.
如图所示,将一张长方形纸片斜折过去,使顶点A落在 A′处,BC为折痕,然后再把BE折过去,使之与BA重合,折痕为BD,若∠ABC=58°,则求∠E′BD的度数是32°.