题目内容
18.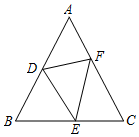 如图,△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且∠B=∠DEF,BD=CE,求证:ED=EF.
如图,△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且∠B=∠DEF,BD=CE,求证:ED=EF.
分析 先根据∠CED=∠B+∠BDE,且∠DEF=∠B,得到∠CEF=∠BDE,再根据ASA判定△BDE≌△CEF,即可得出DE=EF.
解答  证明:∵∠CED是△BDE的外角,
证明:∵∠CED是△BDE的外角,
∴∠CED=∠B+∠BDE,
又∠DEF=∠B,
∴∠CEF=∠BDE,
在△BDE和△CEF中,
$\left\{\begin{array}{l}{∠B=∠C}\\{BD=CE}\\{∠CEF=∠BDE}\end{array}\right.$,
∴△BDE≌△CEF(ASA)
∴DE=EF.
点评 本题主要考查了全等三角形的判定与性质,解决问题的关键是掌握两角及其夹边分别对应相等的两个三角形全等.

练习册系列答案
相关题目
9.已知x,y是实数,$\sqrt{3x+4}$+y2+6y+9=0,若axy-3x=y,则实数a的值是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{7}{4}$ | D. | -$\frac{7}{4}$ |
 如图,等腰直角△ABC中,点A在y轴上,点C在第一象限,∠ABC=90°,OA=3,OB=4,求点C的坐标.
如图,等腰直角△ABC中,点A在y轴上,点C在第一象限,∠ABC=90°,OA=3,OB=4,求点C的坐标.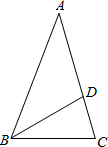 如图,已知△ABC,AB=AC=2,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是$\sqrt{5}$-1.
如图,已知△ABC,AB=AC=2,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是$\sqrt{5}$-1.