题目内容
如图所示．Rt△ABC中，∠A=90°，AD⊥BC于D，EF⊥BC于F．求证：AD•EC=AC•EF．考点：相似三角形的判定与性质
专题：证明题
分析：根据AD⊥BC，EF⊥BC，即可得△ADC∽△EFC，即可得
=
，即可解题．
| AD |
| AC |
| EF |
| EC |
解答：证明：∵AD⊥BC，EF⊥BC，
∴∠ADC=∠EFC，
又∵∠C=∠C，
∴△ADC∽△EFC，
∴
=
，
∴AD•EC=AC•EF．
∴∠ADC=∠EFC，
又∵∠C=∠C，
∴△ADC∽△EFC，
∴
| AD |
| AC |
| EF |
| EC |
∴AD•EC=AC•EF．
点评：本题考查了相似三角形的证明，相似三角形对应边比值相等的性质，本题中求证△ADC∽△EFC是解题的关键．
练习册系列答案
互动英语系列答案
相关题目
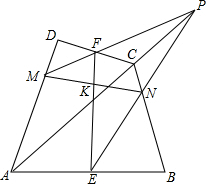如图，四边形中ABCD中，E，F分别是AB，CD的中点，P为对角线AC延长线上的任意一点，PF交AD于M，PE交BC于N，EF交MN于K．
如图△ABC中，∠B=45°，∠C=a（a＞45°），AD是BC边上的高，E是AD上一点且DE=DC，延长BE交AC于F，∠ABF的大小是一轮船从重庆到上海要6天，而从上海到重庆要8天，那么有一木排从重庆顺流漂到上海要（ ）
| A、24天 | B、38天 |
| C、48天 | D、49天 |