题目内容
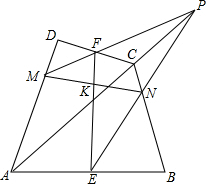如图，四边形中ABCD中，E，F分别是AB，CD的中点，P为对角线AC延长线上的任意一点，PF交AD于M，PE交BC于N，EF交MN于K．求证：K是线段MN的中点．
考点：相似三角形的判定与性质
专题：证明题
分析：根据题意，EF截△PMN，则
.
.
=1(1)；BC截△PAE，则
.
.
=1(2)；所以
=
(3)．而CD截△PMA，则
.
.
=1，即
=
，∴
=
(4)，因AP=AC+CP，得2CP+AC=2AP-AC，由（3），（4）得，
=
，即
.
=1，所以由（1）得NK=KM，即K是线段AM的中点．
| NK |
| KM |
| MF |
| FP |
| PE |
| EN |
| EB |
| BA |
| AC |
| CP |
| PN |
| NE |
| PE |
| EN |
| 2CP+AC |
| AC |
| FD |
| DC |
| CA |
| AP |
| PM |
| MF |
| PM |
| MF |
| 2AP |
| AC |
| PF |
| MF |
| 2AP-AC |
| AC |
| PE |
| EN |
| FP |
| MF |
| MF |
| FP |
| PE |
| EN |
解答：证明：∵EF截△PMN，
则
.
.
=1(1)
∵BC截△PAE，
则
.
.
=1(2)，
∴即有
=
，
所以
=
(3)，
∵CD截△PMA，
则
.
.
=1，
即
=
，∴
=
(4)
因AP=AC+CP，得2CP+AC=2AP-AC，由（3），（4）得，
=
，
即
.
=1，
所以由（1）得NK=KM，即K是线段MN的中点．
则
| NK |
| KM |
| MF |
| FP |
| PE |
| EN |
∵BC截△PAE，
则
| EB |
| BA |
| AC |
| CP |
| PN |
| NE |
∴即有
| PN |
| NE |
| 2CP |
| AC |
所以
| PE |
| EN |
| 2CP+AC |
| AC |
∵CD截△PMA，
则
| FD |
| DC |
| CA |
| AP |
| PM |
| MF |
即
| PM |
| MF |
| 2AP |
| AC |
| PF |
| MF |
| 2AP-AC |
| AC |
因AP=AC+CP，得2CP+AC=2AP-AC，由（3），（4）得，
| PE |
| EN |
| FP |
| MF |
即
| MF |
| FP |
| PE |
| EN |
所以由（1）得NK=KM，即K是线段MN的中点．
点评：本题考查了线段截三角形所得的线段的比为定值．以及比例的性质．
练习册系列答案
阅读快车系列答案
相关题目
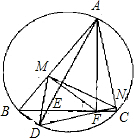如图，在锐角△ABC的BC边上有两点E、F，满足∠BAE=∠CAF，作FM⊥AB，FN⊥AC（M、N是垂足），延长AE交△ABC的外接圆于点D．
如图所示．Rt△ABC中，∠A=90°，AD⊥BC于D，EF⊥BC于F．求证：AD•EC=AC•EF．
如图，在Rt△AOB中，∠AOB=90°，OA=2，OB=1，∠XOA=30°，则A、B两点的坐标分别是