题目内容
14. 如图,把一个长方形纸条ABCD沿EF折叠,若∠BGE=112°,则∠1=56°.
如图,把一个长方形纸条ABCD沿EF折叠,若∠BGE=112°,则∠1=56°.
分析 此题要求∠1的度数,只需根据平行线的性质以及折叠的性质推知∠GEF=∠1,然后由三角形外角定理来求∠1的度数.
解答 解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DEF=∠1,
由折叠的性质得:∠GEF=∠DEF,
∴∠GEF=∠1,
又∵∠BGE=∠1+∠GEF=112°,
∴2∠1=112°,
∴∠1=56°.
故答案为:56.
点评 考查的是平行线的性质、翻折变换(折叠问题),正确观察图形,熟练掌握平行线的性质是解题的关键.

练习册系列答案
相关题目
4.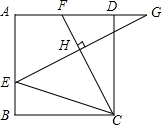 如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )
如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )
 如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )
如图,在边长为3的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG=1,连接EG,CF⊥EG交EG于点H,交AD于点F,则$\frac{FH}{CH}$=( )| A. | 1:1 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1:2 |
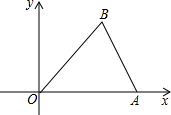 如图,已知A(3,0),B(2,3),将△OAB以点O为位似中心,相似比为2:1,放大得到△OA′B′,则顶点B的对应点B′的坐标为(-4,-6)或(4,6).
如图,已知A(3,0),B(2,3),将△OAB以点O为位似中心,相似比为2:1,放大得到△OA′B′,则顶点B的对应点B′的坐标为(-4,-6)或(4,6).