题目内容
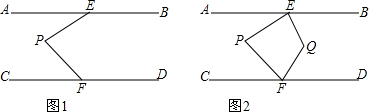
如图1,AB∥CD,在AB、CD内有一条折线EPF.
(1)求证:∠AEP+∠CFP=∠EPF.
(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,∠EPF=α,∠EQF=β,请探究α与β之间的关系,并说明理由.
(1)求证:∠AEP+∠CFP=∠EPF.
(2)如图2,已知∠BEP的平分线与∠DFP的平分线相交于点Q,∠EPF=α,∠EQF=β,请探究α与β之间的关系,并说明理由.

考点:平行线的性质
专题:常规题型
分析:(1)过P点作PG∥AB,根据平行线的性质由PG∥AB得到∠EPG=∠AEP,再根据平行线的性质得PG∥CD,则∠FPG=∠CFP,所以∠AEP+∠CFP=∠EPF;
(2)先根据邻补角的定义得∠BEP=180°-∠AEP,∠DFP=180°-∠CFP,由(1)的结论得∠AEP+∠CFP=α,则∠BEP+∠DFP=360°-α,同样可得∠BEQ+∠DFQ=∠EQF=β,根据角平分线的定义得到∠BEP+∠DFP=2(∠BEQ+∠DFQ),所以360°-α=2β.
(2)先根据邻补角的定义得∠BEP=180°-∠AEP,∠DFP=180°-∠CFP,由(1)的结论得∠AEP+∠CFP=α,则∠BEP+∠DFP=360°-α,同样可得∠BEQ+∠DFQ=∠EQF=β,根据角平分线的定义得到∠BEP+∠DFP=2(∠BEQ+∠DFQ),所以360°-α=2β.
解答:(1)证明: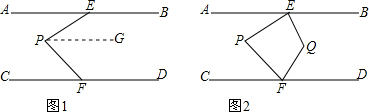 过P点作PG∥AB,如图,
过P点作PG∥AB,如图,
∵PG∥AB,
∴∠EPG=∠AEP,
∵AB∥CD,
∴PG∥CD,
∴∠FPG=∠CFP,
∴∠AEP+∠CFP=∠EPF;
(2)解:α+2β=360°.理由如下:
∵∠BEP=180°-∠AEP,∠DFP=180°-∠CFP,
而∠AEP+∠CFP=α,
∴∠BEP+∠DFP=360°-α,
与(1)一样可得∠BEQ+∠DFQ=∠EQF=β,
而∠BEP的平分线与∠DFP的平分线相交于点Q,
∴∠BEP+∠DFP=2(∠BEQ+∠DFQ),
∴360°-α=2β,
即α+2β=360°.
 过P点作PG∥AB,如图,
过P点作PG∥AB,如图,∵PG∥AB,
∴∠EPG=∠AEP,
∵AB∥CD,
∴PG∥CD,
∴∠FPG=∠CFP,
∴∠AEP+∠CFP=∠EPF;
(2)解:α+2β=360°.理由如下:
∵∠BEP=180°-∠AEP,∠DFP=180°-∠CFP,
而∠AEP+∠CFP=α,
∴∠BEP+∠DFP=360°-α,
与(1)一样可得∠BEQ+∠DFQ=∠EQF=β,
而∠BEP的平分线与∠DFP的平分线相交于点Q,
∴∠BEP+∠DFP=2(∠BEQ+∠DFQ),
∴360°-α=2β,
即α+2β=360°.
点评:本题考查了平行线的性质:平行于同一条直线的两直线平行;两直线平行,内错角相等.

练习册系列答案
相关题目
若点P(x,y)的坐标满足方程组
,则点P不可能在( )
|
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
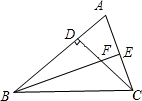 在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,并于CD相交于点F.
在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,并于CD相交于点F.