题目内容
解不等式:2(y+1)+
<
y-1,并把解集在数轴上表示出来.
| y-2 |
| 3 |
| 7 |
| 2 |
考点:解一元一次不等式,在数轴上表示不等式的解集
专题:
分析:去分母、去括号、移项、合并同类项,然后系数化成1即可求解.
解答:解:去分母,得:12(y+1)+2(y-2)<21y-6,
去括号,得:12y+12+2y-4<21y-6,
移项,得:12y+2y-21y<-6-12+4,
合并同类项,得:-7y<-14,
系数化成1得:y>2.
 .
.
去括号,得:12y+12+2y-4<21y-6,
移项,得:12y+2y-21y<-6-12+4,
合并同类项,得:-7y<-14,
系数化成1得:y>2.
 .
.点评:本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 推理填空:
推理填空: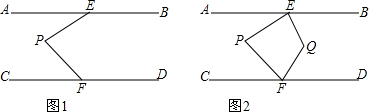
 2014年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1200名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
2014年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1200名学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题: